如图,方格纸上的每个小方格都是边长为1的正方形,我们把格点间连线为边的三角形称为“格点三角形”,图中的△ABC就是一个格点三角形.在△ABC中,BC= ▲ ,tanB= ▲ ;
请在方格中画出一个格点三角形DEF,使
△DEF∽△ABC,并且△DEF与△ABC的相似比为2. 
如图,D,E分别是△ABC的AB,AC边上的点,且DE∥BC,已知AD︰DB=1︰3, DE=2cm,求BC的长.
若△ADE的面积为1.5cm2,求梯形DBCE的面积.

如图,在4×4的正方形网格中,△ABC和 △DEF的顶点都在边长为1的小正方形的顶点上.
△DEF的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC=__________°,BC=__________;
(2)判断△ABC与△DEF是否相似,并证明你的结论.

(本小题满分6分)
如图,某人在点A处测量树高,点A到树的距离AD为21米,将一长为2米的标杆BE在与点A相距3米的点B处垂直立于地面,此时,观察视线恰好经过标杆顶点E及树的顶点C,求此树CD的高.
(本题5分)如图,B是AC上一点,AD⊥AB,EC⊥BC,∠DBE=90°.
求证:△ABD∽△CEB.
在□ABCD中,G为BC延长线上一点,射线AG与直线BD相交于E、与直线CD相交于F.求证:
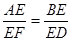 ;
;求证:AE2=E
 F●EG;
F●EG;如果把“G为BC延长线上一点”改为“G为线段BC上一点(不与点B、C重合)”,其它条件不变,(2)中的结论是否成立吗?若成立,请你加以证明;若不成立,请你说明理由。
_如图3,方格纸中的每个小方格都是边长为1的正方形,我们把以格点间连接为边的三角形称为“格点三角形”,图中的△ABC是格点三角形,在建立平面直角坐标系后,点B的坐标为(-2,-2).把△ABC向左平移8格后得到△A1B1C1,画出△A1B1C1的图形,此时点B1的坐为 .
把△ABC绕点C按顺时针方向旋转90°后得到△A2B2C,画出△A2B2C的图形,此时
点B2的坐标为 .把△ABC以点A为位似中心放大为△AB3C3,使放大前后对应边长的比为1︰2,画出△AB3C3的图形.

如图1, 将三角板放在正方形
将三角板放在正方形 上,使三角板的直角顶点
上,使三角板的直角顶点 与正方形
与正方形 的顶点
的顶点 重合,三角扳的一边交
重合,三角扳的一边交 于点
于点 .另一边交
.另一边交 的延长线于点
的延长线于点 .
.求证:
 ;
;如图2,移动三角板,使顶点
 始终在正方形
始终在正方形 的对角线
的对角线 上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理
上,其他条件不变,题(1)中的结论是否仍然成立?若成立,请给予证明:若不成立.请说明理 由:
由:如图3,将(2)中的“正方形
 ”改为“矩形
”改为“矩形 ”,且使三角板的一边经过点
”,且使三角板的一边经过点 ,其他条件不变,若
,其他条件不变,若 、
、 ,求
,求 的值.
的值.
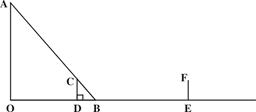
如右图,路灯A离地8米,身高1.6米的小王(C D)的影长DB与身高一样,现在他沿OD方向走10米,到达E处.(1)请画出小王在E处的影子EH;
(2)求EH的长.
(本题满分8分)如图①和图②中每个小正方形的边长都为1个单位长度.
(1)将图①中的格点△ABC(顶点都在网格线交点处的三角形叫做格点三角形)向上平移2个单位长度得到△A1B1C1.请你在图①中画出A1B1C1. (2)在图②中画一个与格点△ABC相似的格点△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.
(2)在图②中画一个与格点△ABC相似的格点△A2B2C2,且△A2B2C2与△ABC的相似比为2:1.
试题篮
()