已知:梯形ABCD中,AD∥BC,∠ABC=90°,BE⊥CD于点E.DP⊥CB于点P,连接AP、PE.如图1,若∠C=45°,求证:AP=  AE.
AE.
如图2,若∠C=60°,直接写出线段AP、AE的数量关系 .
在(1)的条件下,将线段EA绕点E顺时针旋转得到线段EA′,使∠DEA′=∠DAE,直线EA′分别与线段BA延长线、线段BC交于点N、点K,已知AD=1,EK= .求线段NE的长.
.求线段NE的长.
如图,在4×4的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上。请你在图中画出一个与△ABC相似的△DEF,使得△DEF的顶点都在边长为1的小正方形的顶点上,且△ABC与△DEF的相似比为1∶2。
已知:如图,在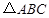 中,D是AC上一点,E是AB上一点,且∠AED =∠C.
中,D是AC上一点,E是AB上一点,且∠AED =∠C.
(1)求证:△AED∽△ACB;
(2)若AB=6,AD= 4,AC=5,求AE的长.
如图,在4×4的正方形方格中,△ABC的顶点都在边长为1的小正方形的顶点上.请你在图中画出一个与△ABC相似的△DEF,使得△DEF的顶点都在边长为1的小正方形的顶点上,且△ABC与△DEF的相似比为1∶2. 
如图,△ABC的顶点在格点上,且点A(-5,-1),点C(-1,-2).
(1)以原点O为旋转中心,将△ABC绕点O逆时针旋转90°得到△ . 请在图中画出△
. 请在图中画出△ ,并写出点A的对称点
,并写出点A的对称点 的坐标;
的坐标;
(2)以原点O为位似中心,位似比为2,在第一象限内将△ABC放大,画出放大后的图形△ .
.
如图:学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成30°角,斜坡CD与水平地面BC成30°的角,求旗杆AB的高度(结果保留根号).
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
求证:△ADF∽△DEC;
若AB=4,AD=3 ,AE=3,求ED,AF的长.
,AE=3,求ED,AF的长.
如图,在 ABCD中,AE∶EB=2∶3.
ABCD中,AE∶EB=2∶3.
(1)求△AEF和△CDF的周长比;
(2)若S△AEF=8cm2,求S△CDF.
如图,BD平分∠ABC,且AB=4,BC=6,则当BD= 时,△ABD∽△DBC.
如图, +1个边长为2的等边三角形有一条边在同一直线上,设
+1个边长为2的等边三角形有一条边在同一直线上,设 的面积为
的面积为 ,
, 的面积为
的面积为 ,…,
,…, 的面积为
的面积为 ,则
,则 =_____. (用含
=_____. (用含 的式子表示).
的式子表示).
网格中每个小正方形的边长都是1.
(1)将图①中的格点三角形ABC平移,使点A平移至点A’,画出平移后的三角形A’B’C’;
(2)在图②中画一个格点三角形DEF,使△DEF∽△ABC,且相似比为2∶1。
试题篮
()