如图，在矩形ABCD中，点E、F分别在边AD、DC上，△ABE∽△DEF，AB=6，AE=9，DE=2，求EF的长.
如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
（1）填空：∠ABC= °，BC= ；
（2）判断△ABC与△DEF是否相似，并证明你的结论.
如图甲,正方形ABCD的边长为2,点M是BC的中点,P是线段MC上的一个动点(不运动至M,C),以AB为直径作⊙O,过点P的切线交AD于点F,切点为E。
(1)求四边形CDFP的周长；(3分)
(2)请连结OF,OP,求证：OF⊥OP；(4分)
(3)延长DC,FP相交于点G,连结OE并延长交直线DC于H(如图乙).是否存在点P
使△EFO∽△EHG(其对应关系是 )?如果存在,试求此时的BP的长；如果不存在,请说明理由。(5分)
如图,已知AB∥CD,AD,BC相交于E,F为EC上一点,且∠EAF=∠C.
求证：(1) ∠EAF=∠B； (2)AF2=FE·FB
如图所示，已知：
中，
．
（1）尺规作图：作
的平分线
交
于点
（只保留作图痕迹，不写作法）；
（2）在（1）所作图形中，将沿某条直线折叠，使点
与点重合，折痕
交
于点
，交
于点
，连接
，再展回到原图形，得到四边形
．
①试判断四边形AEDF的形状，并证明；
②若AC=8,CD=4，求四边形AEDF的周长和BD的长．
已知AB=2，AD=4，∠DAB=90°，AD∥BC（如图）．E是射线BC上的动点（点E与点B不重合），M是线段DE的中点．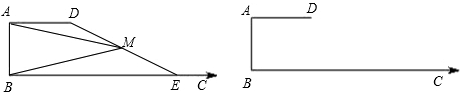
（1）设BE=x，△ABM的面积为y，求y关于x的函数解析式，并写出函数的定义域；
（2）如果以线段AB为直径的圆与以线段DE为直径的圆外切，求线段BE的长；
（3）联结BD，交线段AM于点N，如果以A、N、D为顶点的三角形与△BME相似，求线段BE的长．
已知：在△ABC中，∠ACB=900，点P是线段AC上一点，过点A作AB的垂线，交BP的延长线于点M，MN⊥AC于点N，PQ⊥AB于点Q，A0=MN．
（1）如图l，求证：PC=AN；
（2） 如图2，点E是MN上一点，连接EP并延长交BC于点K，点D是AB上一点，连接DK，∠DKE=∠ABC，EF⊥PM于点H，交BC延长线于点F，若NP=2，PC=3，CK：CF=2：3，求DQ的长．
如图在边长为2的圆内接正方形ABCD中，AC是对角线，P为边CD的中点，延长AP交圆于点E 
（1）写出同圆中一对不全等的相似三角形，并说明理由
（2）求弦DE的长。
锐角△ABC中，BC=6，
，两动点M,N分别在边AB,AC上滑动，且MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y(y＞0)．
(1) 求△ABC中边BC上高AD；
(2) 当
为何值时，PQ恰好落在边BC上（如图1）；
(3) 当PQ在
外部时（如图2），求y关于x的函数关系式（注明x的取值范围），并求出x为何值时y最大，最大值是多少？
如图，在△ABC中，AD、CE是两条高，连结DE，如果BE=2，EA=3，CE=4，在不添加任何辅助线和字母的条件下，请写出三个正确结论 （要求：分别为边的关系，角的关系，三角形相似的关系），并对其中三角形相似的结论给予证明.
边的关系 ;
角的关系 ;
三角形相似的关系 .
证明:
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB.
(1)求证：AD⊥DC
(2)若AD＝2，AC＝
,求AB的长．
如图，小明晚上由路灯A下的B处走到C处时，测得影子CD的长为1米，从C处继续往前走2米到达E处时，测得影子EF的长为2米，Ｂ、Ｃ、Ｄ、Ｅ、Ｆ在同一条直线上，已知小明的身高是1．6米，求路灯A的高度？
如图，AD是
ABC的高，点P，Q在BC边上，点R在AC边上，点S在AB边上，BC=60cm，AD=40cm，AB=AC.四边形PQRS是正方形。
（1）ASR与ABC相似吗？为什么？
（2）求正方形PQRS的边长。
如图，将矩形ABCD沿两条较长边的中点的连线对折，得到的矩形EADF与矩形ABCD相似，确定矩形ABCD长与宽的比。
如图，四边形ABCD、CDEF、EFGH都是正方形.
(1)
ACF与ACG相似吗？说说你的理由.
(2)求∠1+∠2的度数.
试题篮
()
粤公网安备 44130202000953号
