初中数学相似多边形的性质解答题

已知：如图，在△ABC中，∠ACB=，过点C作CD⊥AB于点D，点E为AC上一点，过E点作AC的垂线，交CD的延长线于点F ，与AB交于点G.求证：△ABC∽△FGD

如图1, 矩形铁片ABCD中，AD="8," AB="4;" 为了要让铁片能穿过直径为3.8的圆孔, 需对铁片进行处理 (规定铁片与圆孔有接触时铁片不能穿过圆孔).
(1)直接写出矩形铁片ABCD的面积           ；
(2)如图2, M、N、P、Q分别是AD、AB、BC、CD的中点,将矩形铁片的四个角去掉.
①证明四边形MNPQ是菱形；
②请你通过计算说明四边形铁片MNPQ能穿过圆孔.
(3)如图3, 过矩形铁片ABCD的中心作一条直线分别交边BC、AD于点E、F(不与端点重合), 沿着这条直线将矩形铁片切割成两个全等的直角梯形铁片.当BE=DF=1时,判断直角梯形铁片EBAF能否穿过圆孔, 并说明理由.

在△ABC中,∠C＝90°
（1）如图1,P是AC上的点,过点P作直线截△ABC,使截得的三角形与△ABC相似.
例如：过点P作PD∥BC交AB于D,则截得的△ADP与△ABC相似.请你在图中画出所有满足条件的直线.
（2）如图2,Q是BC上异于点B,C的动点,过点Q作直线截△ABC,使截得的三角形与△ABC相似,直接写出满足条件的直线的条数.(不要求画出具体的直线)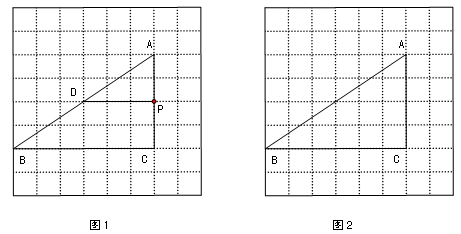

如图所示：直线MN⊥RS于点O，点B在射线OS上，OB=2，点C在射线ON上，OC=2，点E是射线OM上一动点，连结EB，过O作OP⊥EB于P，连结CP，过P作PF⊥PC交射线OS于F。
（1）求证：△POC∽△PBF。
（2）当OE=1，OE=2时， BF的长分别为多少？当OE=n时，BF=_______.
（3）当OE=1时，；OE=2时， ；…,OE=n时，.则=_______.（直接写出答案）

备用图

如图，在平面直角坐标系中，点A，C分别在x轴，y轴上，四边形ABCO
为矩形，AB=16，点D与点A关于y轴对称，tan∠ACB=，点E，F分别是线段AD，AC上的动点（点
E不与点A，D重合），且∠CEF=∠ACB。
（1）求AC的长和点D的坐标；
（2）说明△AEF与△DCE相似；
（3）当△EFC为等腰三角形时，求点E的坐标。

如图所示，一段街道的两边缘所在直线分别为AB、PQ，并且AB∥PQ．建筑物的一端DE所在的
直线MN⊥AB于点M，交PQ于点N．小亮从胜利街的A处，沿着AB方向前进，小明一直站在点P的位置等
候小亮．
（1）请你在图中画出小亮恰好能看见小明时的视线，以及此时小亮所在位置（用点C标出）；
（2）已知：MN=20m，MD=8m，PN=24m，求（1）中的点C到胜利街口的距离CM．

定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形.
探究：（1）如图甲，已知△ABC中∠C=90°，你能把△ABC分割成2个与它自己相似的小直角三角形吗？若能，请在图甲中画出分割线，并说明理由.
（2）一般地，“任意三角形都是自相似图形”，只要顺次连结三角形各边中点，则可将原三分割为四个都与它自己相似的小三角形．我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割，称为2阶分割（如图2）……依次规则操作下去．n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为S_n．
①若△DEF的面积为1000，当n为何值时，3<S_n<4?
（请用计算器进行探索，要求至少写出二次的尝试估算过程）
②当n>1时，请写出一个反映S_n-1,S_n,S_n+1之间关系的等式（不必证明）

如图，△ABC中， BE⊥AC于E,AD⊥BC于D.求证：△CDE∽ △CAB
  

（1）(3分)如图（1），正方形AEGH的顶点E、H在正方形ABCD的边上，直接写出HD∶GC∶EB的结果（不必写计算过程）；
（2）(3分)将图（1）中的正方形AEGH绕点A旋转一定角度，如图（2），求HD∶GC∶EB；
（3）(2分)把图（2）中的正方形都换成矩形，如图（3），且已知ＤA∶AB＝HA∶AE＝m: n，此时HD∶GC∶EB的值与（2）小题的结果相比有变化吗？如果有变化，直接写出变化后的结果（不必写计算过程）．

如图，在矩形ABCD中，AB=6，AD=12，点E在AD边上，且AE=8，EF⊥BE交CD于F．
（1）求证：△ABE∽△DEF；
（2）求EF的长．

如图，为测量学校围墙外直立电线杆AB的高度，小亮在操场上点C处直立高3m的竹竿CD，然后退到点E处，此时恰好看到竹竿顶端D与电线杆顶端B重合；小亮又在点C₁处直立高3m的竹竿C₁D₁，然后退到点E₁处，此时恰好看到竹竿顶端D₁与电线杆顶端B重合。小亮的眼睛离地面高度EF=1.5m，量得CE=2m，EC₁=6m，C₁E₁=3m。
（1）△FDM∽△    ▲   ，△F₁D₁N∽△    ▲   ；
（2）求电线杆AB的高度。

如图，在平面直角坐标系O中，矩形AOCD的顶点A的坐标是（0,4），现有两动点P、Q，点P从点O出发沿线段OC（不包括端点O，C）以每秒2个单位长度的速度，匀速向点C运动，点Q从点C出发沿线段CD（不包括端点C，D）以每秒1个单位长度的速度匀速向点D运动.点P，Q同时出发，同时停止，设运动时间为t秒，当t=2秒时PQ=.

（1）求点D的坐标，并直接写出t的取值范围；
（2）连接AQ并延长交轴于点E,把AE沿AD翻折交CD延长线于点F,连接EF，则△AEF的面积S是否随t的变化而变化？若变化，求出S与t的函数关系式；若不变化，求出S的值.
（3）在（2）的条件下，t为何值时，四边形APQF是梯形？

如图，三角形ABC的两个顶点B、C在圆上，顶点A在圆外，AB、AC分别交圆于E、D两点，连结EC、BD．
(1)求证：ΔABD∽ΔACE；
(2)若ΔBEC与ΔBDC的面积相等，试判定三角形ABC的形状．

如图，在正方形ABCD中，E是BC上的一点,连结AE，作BF⊥AE，垂足为H,交CD于F,作CG∥AE,交BF于G.
求证：（1） CG=BH；（2）FC²=BF·GF；（3）.

在△ABC中，∠A＝90°，AB＝4，AC＝3，M是AB上的动点（不与A，B重合），过M点作MN∥BC交AC于点N．以MN为直径作⊙O，并在⊙O内作内接矩形AMPN．令AM＝x．  
（1）用含x的代数式表示△ＭNP的面积S；     
（2）当x为何值时，⊙O与直线BC相切？      
（3）在动点M的运动过程中，记△ＭNP与梯形BCNM重合的面积为y，试求y关于x的函数表达式.