如图①,将一个内角为120°的菱形纸片沿较长对角线剪开,得到图②的两张全等的三角形纸片.将这两张三角形纸片摆放成图③的形式.点B、F、C、D在同一条直线上,AB分别交DE、EF于点P、M,AC交DE于点N.
(1)求证:△APN≌△EPM.
(2)连接CP,试确定△CPN的形状,并说明理由.
(3)当P为AB的中点时,求△APN与△DCN的面积比.
如图,四边形ABCD是正方形,△ECF是等腰直角三角形,其中CE=CF,G是CD与EF的交点.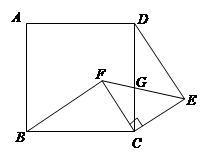
(1)求证:△BCF≌△DCE;
(2)若BC=5,CF=3,∠BFC=90°,求DG︰GC的值.
如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥CO. 
(1)试说明△ADB与△OBC相似.
(2)若AB=2,BC= ,求AD的长.(结果保留根号)
,求AD的长.(结果保留根号)
如图,在正方形网格中,△OBC的顶点分别为O(0,0), B(3,-1)、C(2,1).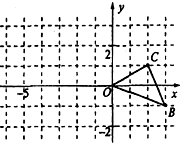
(1)以点O(0,0)为位似中心,按比例尺2:1在位似中心的异侧将△OBC放大为△OB′C′,放大后点B、C两点的对应点分别为B′、C′ ,画出△OB′C′,并写出点B′、C′的坐标:B′( , ),C′( , );
(2)在(1)中,若点M(x,y)为线段BC上任一点,写出变化后点M的对应点M′的坐标( , ).
如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CPQ与△CBA相似,所需要的时间是多少秒?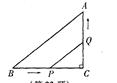
如图,△ABC是等边三角形,点D、E分别在BC、AC上,且BD=CE,AD与BE相交于点F.(1)试说明:△ABD≌△BCE. (2)△AEF与△ABE相似吗?请说明理由.
(3)试说明:BD2=AD·DF.
有一块直角三角形木板如图所示,已知∠C=90°,BC=3cm, AC=4cm.根据需要,要把它加工成一个正方形木板,小明和小丽分别设计了如图1和图2的两种方法,哪一块正方形木板面积更大?请说明理由.
△ABC是一块等边三角形的废铁片,利用其剪裁一个正方形DEFG,使正方形的一条边DE落在BC上,顶点F、G分别落在AC、AB上.
(1) 证明:△BDG≌△CEF;
(2) 设△ABC的边长为2,请你帮小聪求出正方形的边长.(结果精确到十分位)
(3) 小颖想:不求正方形的边长我也能画出正方形.具体作法是:如图3
①在AB边上任取一点G′,如图作正方形G′D′E′F′;
②连接BF′并延长交AC于F;
③作FE∥F′E′交BC于E,FG∥F′G′交AB于G,GD∥G′D′交BC于D,则四边形DEFG即为所求.你认为小颖的作法正确吗?请说明理由.
九年级上册的教材第118页有这样一道习题:
“在一块三角形余料ABC中,它的边BC=120mm,高线AD=80mm.要把它加工成正方形零件(如图),使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长为多少mm?”
(1)请你解答上题;
(2)若将上题图中的正方形PQMN改为矩形,其余条件不变,求矩形PQMN的面积S的最大值;
(3)我们把上面习题中的正方形PQMN叫做“BC边上的△ABC的内接正方形”,若在习题的条件下,又知AB=150mm,AC=100mm,请分别写出AB边上的△ABC的内接正方形的边长和AC边上的△ABC的内接正方形的边长(不必写出过程,只要直接写出答案即可,结果精确到1mm);
(4)结合第(1)、(3)题,若三角形的三边长分别为a,b,c,各边上的高分别为ha,hb,hc,要使a边上的三角形内接正方形的面积最大,请写出a与ha必须满足的条件(不必写出过程). 
如图,在梯形ABCD中,AD∥BC, AB = CD,E是AD的中点,AD=4,BC=6,点P是BC边上的动点(不与点B重合),PE与BD相交于点O,设PB的长为x.
(1) 当P点在BC边上运动时,求证:△BOP∽△DOE.
(2) 当x = ( )时,四边形ABPE是平行四边形;当x = ( )时,四边形ABPE是直角梯形;
(3)当P在BC上运动的过程中,四边形ABPE会不会是等腰梯形?试说明理由.
如图,一块直角三角板的直角顶点P放在正方形ABCD的BC边上,并且使一条直角边经过点D,另一条直角边与AB交于点Q. 
(1)请你写出一对相似三角形,并加以证明;
(2)当点P满足什么条件时,  ,请证明你的结论;
,请证明你的结论;
图是小红设计的钻石形商标,△ABC是边长为2的等边三角形,四边形ACDE是等腰梯形,AC∥ED,∠EAC=60°,AE=1.
(1)证明:△ABE≌△CBD;
(2)图中存在多对相似三角形,请你找出一对进行证明,并求出其相似比(不添加辅助线,不找全等的相似三角形);
(3)小红发现AM=MN=NC,请证明此结论;
(4)求线段BD的长.
如图,BD是⊙O的直径, A、C是⊙O上的两点,且AB=AC,AD与BC的延长线交于点E.
(1)求证:△ABD∽△AEB;
(2)若AD=1,DE=3,求BD的长. 
阅读理解:如图1,在直角梯形ABCD中,AB∥CD,∠B=900,点P在BC边上,当
∠APD=900时,易证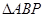 ∽
∽ ,从而得到
,从而得到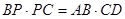 ,解答下列问题.
,解答下列问题.
(1)模型探究1:如图2,在四边形ABCD中,点P在BC边上,当∠B=∠C=∠APD时, 结论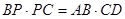 仍成立吗? 试说明理由;
仍成立吗? 试说明理由;
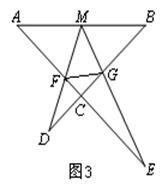
(2)拓展应用:如图3,M为AB的中点,AE与BD交于点C,∠DME=∠A=∠B=45°且DM交AC于F,ME交BC于G.AB=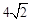 ,AF=3,求FG的长.
,AF=3,求FG的长.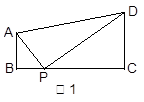
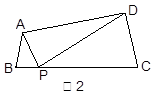
试题篮
()