初中数学相似多边形的性质解答题

如图所示，图中的小方格都是边长为1的正方形，△ABC与△A'B'C'是以点O为位似中心的位似图形，它们的顶点都在小正方形的顶点上．

（1）画出位似中心点O；
（2）直接写出△ABC与△A′B′C′的位似比_______ 
（3）以位似中心O为坐标原点，以格线所在直线为坐标轴建立平面直角坐标系，画出△A′B′C′关于点O中心对称的△A″B″C″，并直接写出△A″B″C″各顶点的坐标．_______；_______；_______

如图，正方形ABCD中，E为AB的中点，AF⊥DE于点O， 则等于      

（本小题满分12分）如图所示，△ABC和△DEF是两个全等的等腰直角三角形，∠BAC=∠EDF=90°，△DEF的顶点E与△ABC的斜边BC的中点重合．将△DEF绕点E旋转，旋转过程中，线段DE与线段AB相交于点P，线段EF与射线CA相交于点Q．
（1）如图①，当点Q在线段AC上，且AP=AQ时，求证：△BPE≌△CQE；
（2）如图②，当点Q在线段CA的延长线上时，求证：△BPE∽△CEQ；并求当BP=a，CQ=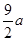时，P、Q两点间的距离 （用含a的代数式表示）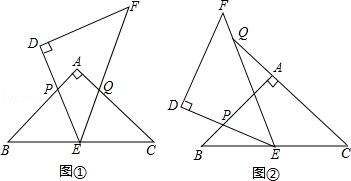

如图，在每个小正方形的边长为1的网格中，点A， B， C， D均在格点上，点E， F分别为线段BC，DB上的动点，且BE =DF．
（Ⅰ）如图①，当BE =时，计算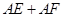的值等于              ；
（Ⅱ）当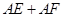取得最小值时，请在如图②所示的网格中，用无刻度的直尺，画出线段AE，AF，并简要说明点E和点F的位置是如何找到的（不要求证明）      ．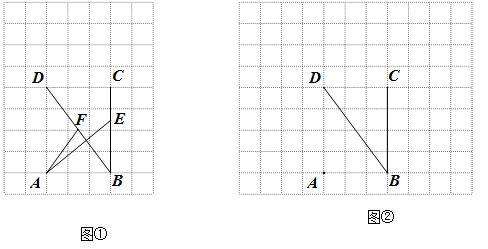

如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D为边CB上的一个动点（点D不与点B重合），过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD．

（1）求证：△DOB∽△ACB；
（2）若AD平分∠CAB，求线段BD的长；
（3）当△AB′D为等腰三角形时，求线段BD的长．

如图，在△ABC中，AB=AC，∠A=36°，BD为角平分线，DE⊥AB，垂足为E．

（1）写出图中一对全等三角形和一对相似比不为1的相似三角形；
（2）选择（1）中一对加以证明．

如图，在平面直角坐标系中放置一顶点为A，B，O的直角三角形，将此三角形绕原点O顺时针旋转90°得到△A₁B₁O．抛物线y=-x²+x+2经过A，B，B₁三点．

（1）求直线A₁B₁的解析式；
（2）设点C是在抛物线上第一象限内的一点，△COB₁的面积是△ABO面积的2倍，求C点坐标；
（3）线段AB上是否存在一点P，使以点P，A₁，B为顶点的三角形与△ABO相似？若存在，请求出的值；若不存在，请说明理由．

如图，在 $△ABC$中，点 $D$、 $E$、 $F$分别在 $AB$、 $BC$、 $AC$上，且 $\angle ADF+\angle DEC=180°$， $\angle AFE=\angle BDE$．

（1）如图1，当 $DE=DF$时，图1中是否存在于 $AB$相等的线段？若存在，请找出并加以证明．若不存在说明理由．
（2）如图2，当 $DE=kDF$（其中 $0<k<1$）时，若 $\angle A=90°$， $AF=m$，求 $BD$的长（用含 $K$， $M$的式子表示）．

如图1，在△ABC中，∠C=90°，点D在AC上，且CD>DA，DA=2．点P、Q同时从D点出发，以相同的速度分别沿射线DC、射线DA运动．过点Q作AC的垂线段QR，使QR=PQ，联接PR．当点Q到达A时，点P、Q同时停止运动．设PQ=x．△PQR和△ABC重合部分的面积为S．S关于x的函数图像如图2所示（其中0<x≤，<x≤m时，函数的解析式不同）
（1）填空：n的值为___________;
（2）求S关于x的函数关系式，并写出x的取值范围．

如图，正方形ABCD中，M为BC上一点，F是AM的中点，EF⊥AM，垂足为F，交AD的延长线于点E，交DC于点N．

（1）求证：△ABM∽△EFA；
（2）若AB=12，BM=5，求DE的长．

． 如图，已知点E是矩形ABCD的边CD上一点，BF⊥AE于点F，
求证：△ABF∽△EAD．

如下图，路灯下，一墙墩（用线段AB表示）的影子是BC，小明（用线段DE表示）的影子是EF，在M处有一颗大树，它的影子是MN。

（1）试确定路灯的位置（用点P表示）。
（2）在图中画出表示大树高的线段。
（3）若小明的眼睛近似地看成是点D，试画图分析小明能否看见大树。

（1）如图1是某个多面体的表面展开图．
①请你写出这个多面体的名称，并指出图中哪三个字母表示多面体的同一点；
②如果沿BC、GH将展开图剪成三块，恰好拼成一个矩形，那么△BMC应满足什么条件？（不必说理）
（2）如果将一个三棱柱的表面展开图剪成四块，恰好拼成一个三角形，如图2，那么该三棱柱的侧面积与表面积的比值是多少？为什么？（注：以上剪拼中所有接缝均忽略不计）

如图1，在Rt△ABC中，∠ACB＝90°，AC＝6，BC＝8，点D在边AB上运动，DE平分∠CDB交边BC于点E，EM⊥BD垂足为M，EN⊥CD垂足为N．

（1）当AD＝CD时，求证DE∥AC；
（2）探究：AD为何值时，以B，M，E为顶点的三角形与以C，E，N为顶点的三角形相似？

如图，以O为圆心的度数为60 ^o，∠BOE=45^o，DA⊥OB，EB⊥OB．

（1）求的值；
（2）若OE与交于点M，OC平分∠BOE，连接CM．说明：CM为⊙O的切线；
（3）在（2）的条件下，若BC=1，求tan∠BCO的值．