好学的小宸利用电脑作了如下的探索:
(1)如图①,将边长为2的等边三角形复制若干个后向右平移,使一条边在同一直线上.则△A2C1B1的面积为 ;
(2)求△A4C3B3的面积;
(3)在保持图①中各三角形的边OB1=B1B2=B2B3=B3B4=2不变的前提下,小宸又作了如下探究:将顶点A1、A2、A3、A4向上平移至同一高度(如图②),若OA4=OB4,试判断以OA2、OA3和OA4为三边能否构成三角形?若能,请判断这个三角形的形状;若不能,请说明理由.
如图,在矩形ABCD中,AB=4,BC=3,将矩形绕点C按顺时针方向旋转,使点B落在线段AC上,得矩形CEFG,边CD与EF交于点H,连接DG.
(1)CH= .
(2)求DG的长.
如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F是DE与AC的交点,且DF=FE.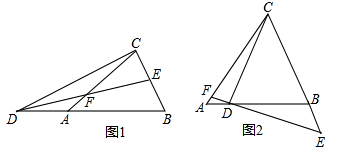
(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;
(2)求证:BE=EC;
(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).

如图,方形ABCD的AB边为直径,在正方形内部作半圆,圆心为O,DF切半圆于点E,交AB的延长线于点F,BF=4.求:
cos∠F的值;BE的长.
如图,在⊙O的内接△ABC中,∠ACB=90°,AC=2BC,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是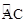 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:△PAC∽△PDF;
(2)若AB=5,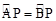 ,求PD的长;
,求PD的长;
(3)在点P运动过程中,设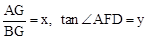 ,求
,求 与
与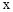 之间的函数关系式.(不要求写出
之间的函数关系式.(不要求写出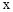 的取值范围)
的取值范围)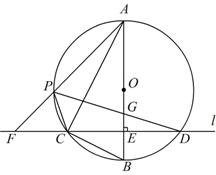
如图,在梯形ABCD中,AD∥BC,AD=3,DC=5,AB=4 ,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.
,∠B=45°.动点M从B点出发沿线段BC以每秒2个单位长度的速度向终点C运动;动点N同时从C点出发沿线段CD以每秒1个单位长度的速度向终点D运动.设运动的时间为t秒.求BC的长
当MN∥AB时,求t的值
试探究:t为何值时,△MNC为等腰三角形.

如图,矩形ABCD中,AB=20,BC=10,点P为AB边上一动点,DP交AC于点Q.
(1)求证:△APQ∽△CDQ;
(2)P点从A点出发沿AB边以每秒1个单位的速度向B点移动,移动时间为t秒.
①当t为何值时,DP⊥AC?
②设 ,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
,写出y与t之间的函数解析式,并探究P点运动到第几秒到第几秒之间时,y取得最小值.
已知:如图,在平面直角坐标系中,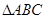 是直角三角形,
是直角三角形,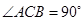 ,点
,点 的坐标分别为
的坐标分别为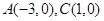 ,
,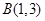
求过点
 的直线的函数表达式
的直线的函数表达式在
 轴上找一点
轴上找一点 ,连接
,连接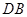 ,使得
,使得 与
与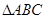 相似(不包括全等),并求点
相似(不包括全等),并求点 的坐标;
的坐标;在⑵的条件下,如
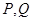 分别是
分别是 和
和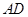 上的动点,连接
上的动点,连接 ,设
,设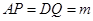 ,问是否存在这样的
,问是否存在这样的 使得
使得 与
与 相似,如果存在,请求出
相似,如果存在,请求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
解决问题:如图,已知正方形ABCD,点E是边AB上一动点,点F在AB边或其延长线上,点G在边AD上.连结ED,FG,交点为H.如图1,若AE=BF=GD,请直接写出∠EHF= ▲ °;
如图2,若EF =
 CD,GD=
CD,GD= AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出tanα.
AE,设∠EHF=α.请判断当点E在AB上运动时, ∠EHF的大小是否发生变化?若发生变化,请说明理由;若不发生变化,请求出tanα. 

如图(1),(2)所示,矩形ABCD的边长AB=6,BC=4,点F在DC上,DF=2。
动点M、N分别从点D、B同时出发,沿射线DA、线段BA向点A的方向运动(点M可
运动到DA的延长线上),当动点N运动到点A时,M、N两点同时停止运动。连接FM、
FN,当F、N、M不在同一直线时,可得△FMN,过△FMN三边的中点作△PQW。设动点
M、N的速度都是1个单位/秒,M、N运动的时间为x秒。试解答下列问题:
(1)说明△FMN∽△QWP;
(2)设0≤x≤4(即M从D到A运动的时间段)。试问x为何值时,△PQW为直角三角形?
当x在何范围时,△PQW不为直角三角形?
(3)问当x为何值时,线段MN最短?求此时MN的值。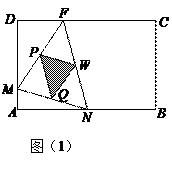

如图,在△ 中,∠
中,∠ 90°,
90°, ,
, ,点
,点 从点
从点 出发,沿
出发,沿 以
以
2㎝ 的速度向点
的速度向点 移动,点
移动,点 从点
从点 出发,以
出发,以 的速度向点
的速度向点 移动,若点
移动,若点 分别从点
分别从点 同时出发,
同时出发,
设运动时间为 ,当
,当 为何值时,△
为何值时,△ 与△
与△ 相似?
相似?
如图,AB是⊙O的直径,C、P是 上两点,AB=13,AC=5,
上两点,AB=13,AC=5,
(1)如图(1),若点P是 的中点,求PA的长;
的中点,求PA的长;
(2)如图(2),若点P是 的中点,求PA得长 .
的中点,求PA得长 .
如图,已知直线 分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
分别与y轴,x轴交于A,B两点,点M在y轴上,以点M为圆心的圆M与直线AB相切于点D,连结MD.
(1)求证:
 ∽
∽ ;
;
(2)如果圆M的半径为 ,请求出点M的坐标,并写出以
,请求出点M的坐标,并写出以 为顶点,且过点M的抛物线的解析式;
为顶点,且过点M的抛物线的解析式;
(3)在(2)的条件下,试问此抛物线上是否存在点P,使得以P、A、M三点为顶点的三角形与 相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
相似,如果存在,请求出所有符合条件的点P的坐标,如果不存在,请说明理由。
如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为3,AD="4" ,求AC的长.
试题篮
()