如图,在边上为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移 5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)求△CC1C2的面积.
小明、小亮利用灯光下自己的影子长度来测量一路灯的高度,并探究影子长度的变化规律.如图,在同一时间,身高为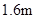 的小明
的小明 的影子
的影子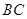 长是
长是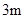 ,而小亮
,而小亮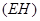 刚好在路灯灯泡的正下方
刚好在路灯灯泡的正下方 点,并测得
点,并测得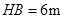 .
.
(1)请在图中画出形成影子的光线,交确定路灯灯泡所在的位置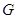 ;
;
(2)求路灯灯泡的垂直高度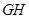 .
.
如图,一条河的两岸有一段是平行的,在河的南岸边每隔 米有一棵树,在北岸边每隔
米有一棵树,在北岸边每隔 米有一根电线杆.小丽站在离南岸边
米有一根电线杆.小丽站在离南岸边 米的点
米的点 处看北岸,发现北岸相邻的两根电线杆A、B,恰好被南岸的两棵树C、D遮住,并且在这两棵树之间还有三棵树,求河的宽度.
处看北岸,发现北岸相邻的两根电线杆A、B,恰好被南岸的两棵树C、D遮住,并且在这两棵树之间还有三棵树,求河的宽度.
如图,九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度 ,标杆与旗杆的水平距离
,标杆与旗杆的水平距离 ,人的眼睛与地面的高度
,人的眼睛与地面的高度 ,人与标杆
,人与标杆 的水平距离
的水平距离 ,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆
,人的眼睛E、标杆顶点C和旗杆顶点A在同一直线,求旗杆 的高度.
的高度.

如图,将△ABC在网格中(网格中每个小正方形的边长均为1)依次进行位似变换、轴对称变换和平移变换后得到△A1B1C1.

(1)△ABC与△A1B1C1的位似比等于 ;
(2)在网格中画出△A1B1C1关于y轴的轴对称图形△A2B2C2;
(3)请写出△A1B1C1是由△A2B2C2怎样平移得到的?
(4)设点P(x,y)为△ABC内一点,依次经过上述三次变换后,点P的对应点的坐标为 .
如图,在边长为1的正方形网格中,有一格点△ABC,已知A、B、C三点的坐标分别是A(1,0)B(2,-1)C(3,1).



(1)请在网格图形中画出平面直角坐标系;
(2)以原点O为位似中心,将△ABC放大2倍,画出放大后的△A′B′C′;
(3)写出△A′B′C′各顶点的坐标:A′____,B′____,C′ ___;
在一个边长为a(单位:cm)的正方形ABCD中,点E、M分别是线段AC,CD上的动点,连结DE并延长交正方形的边于点F,过点M作MN⊥DF于H,交AD于N.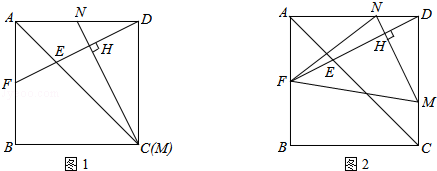
(1)如图1,当点M与点C重合,求证:DF=MN;
(2)如图2,假设点M从点C出发,以1cm/s的速度沿CD向点D运动,点E同时从点A出发,以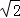 cm/s速度沿AC向点C运动,运动时间为t(t>0);
cm/s速度沿AC向点C运动,运动时间为t(t>0);
①判断命题“当点F是边AB中点时,则点M是边CD的三等分点”的真假,并说明理由.
②连结FM、FN,△MNF能否为等腰三角形?若能,请写出a,t之间的关系;若不能,请说明理由.
已知四边形ABCD中,E、F分别是AB、AD边上的点,DE与CF交于点G.
(1)如图①,若四边形ABCD是矩形,且DE⊥CF,求证 ;
;
(2)如图②,若四边形ABCD是平行四边形,试探究:当∠B与∠EGC满足什么关系时,使得 成立?并证明你的结论;
成立?并证明你的结论;
(3)如图③,若BA=BC=6,DA=DC=8,∠BAD=90°,DE⊥CF,请直接写出 的值.
的值.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B
(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6 ,AF=4
,AF=4 ,求AE的长.
,求AE的长.
如图,△ABC三个定点坐标分别为A(﹣1,3),B(﹣1,1),C(﹣3,2).
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)以原点O为位似中心,将△A1B1C1放大为原来的2倍,得到△A2B2C2,请在第三象限内画出△A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.
已知,如图,以点P(﹣1,0)为圆心的圆,交x轴于A、C两点(A在C的左侧),交y轴于B、D两点(B在D的上方),且∠BAC=30°,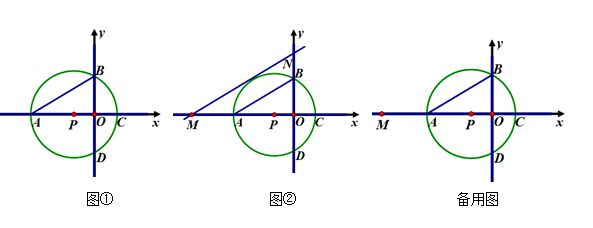
(1)如图①求⊙P的半径及点B的坐标;
(2)点Q是⊙P上任意一点,求△ABQ面积S的取值范围;
(3)如图②,已知点M(-5,0),过M作直线y=kx+b交y轴于点N,
①若MN//AB,试判断MN与⊙P的位置关系,并说明理由;
②在该直线上存在一点G,使以G、A、C为顶点的三角形是直角三角形,且满足条件的点G有且只有三个不同位置,求直线MN的函数关系式.
阅读:如图1,在△ABC中,BE是AC边上的中线, D是BC边上的一点,CD:BD=1:2,AD与BE相交于点P,求 的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).
的值.小昊发现,过点A作AF∥BC,交BE的延长线于点F,通过构造△AEF,经过推理和计算能够使问题得到解决(如图2).


(1) 的值为 ;
的值为 ;
(2)参考小昊思考问题的方法,解决问题:
如图3,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC:AC=1:2:3 .
 求
求 的值;
的值;
 若CD=2,求BP的长.
若CD=2,求BP的长.

试题篮
()