初中数学相似多边形的性质填空题

在比例尺1∶10 000 000的地图上，量得甲、乙两个城市之间的距离是8 cm，那么甲、乙两个城市之间的实际距离应为         km。

如图，已知Rt△ABC，D₁是斜边AB的中点，过D₁作D₁E₁⊥AC于E₁，连结BE₁交CD₁于D₂；过D₂作D₂E₂⊥AC于E₂，连结BE₂交CD₁于D₃；过D₃作D₃E₃⊥AC于E₃，…，如此继续，可以依次得到点E₄、E₅、…、E_n，分别记△BCE₁、△BCE₂、△BCE₃···△BCE_n的面积为S₁、S₂、S₃、…S_n. 则S_n＝ ▲  S_△ABC（用含n的代数式表示）．

如图，点P是矩形ABCD的边AD的一个动点，矩形的两条边AB、BC的长分别为3和4，那么点P到矩形的两条对角线AC和BD的距离之和是＿＿

如图，小红作出了边长为1的第1个正三角形△A₁B₁C₁，算出了正△A₁B₁C₁的面积，然后分别取△A₁B₁C₁三边的中点A₂B₂C₂，作出了第二个正三角形△A₂B₂C₂，算出第2个正△A₂B₂C₂的面积，用同样的方法作出了第3个正△A₃B₃C₃，算出第3个正△A₃B₃C₃的面积，依此方法作下去，由此可得第n次作出的正△A_nB_nC_n的面积是　　．

、若四边形ABCD与四边形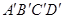的相似比为3∶2，那么四边形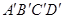与四边形ABCD的相似比为       。

如图，直角三角形ABC中，∠ACB=90⁰，AB=10， BC=6，在线段AB上取一点D，作DF⊥AB交AC于点F.现将△ADF沿DF折叠，使点A落在线段DB上，对应点记为A₁；AD的中点E的对应点记为E₁.若△E₁FA₁∽△E₁BF，则AD=       .

如图，□ABCD中，E是AB中点，F在AD上，且AF＝FD，EF交AC于G，则AG︰AC＝______．

如图，CD是⊙O的直径，弦AB⊥CD，垂足为点M，AB=20，分别以DM、CM为直径作两个大小不同和⊙O₁和⊙O₂，则图中所示阴影部分的面积为          .（结果保留）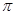

如图，在正六边形ABCDEF与正六边形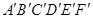中

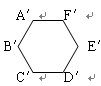
∵正六边形的每个内角都等于120°
∴∠A=∠A′，         ，        ，
，         ，         ；
又∵AB=BC=CD=DE=EF=FA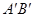
=                        ；
∴=                            ＇
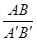∴正六边形ABCDEF∽正六边形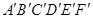

、如图，四边形ABCD和四边形A1B1C1D1相似，已知∠A=120°，∠B=85°
∠C1=75°，AB=10，A1B1=16，CD=18，则∠D1=     ，C1D1=     ，它们的相似比为      。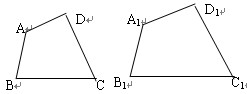

如图所示，在△ABC中，BC=6，E、F分别是AB、AC的中点，动点P在射线EF上，BP交CE于D，∠CBP的平分线交CE于Q，当CQ=CE时，EP+BP=            ．

如图，AB是⊙O的直径，弦BC=4㎝，F是弦BC的中点，∠ABC=60°，若动点E以1 ㎝/s的速度从A点出发在AB上沿着A→B→A运动，设运动时间为t（s）（0≤t＜16），连接EF，当△BEF是直角三角形时，t（s）的值为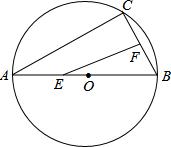                 

如图，平行四边形ABCD中，AB=5，AD=7，AB⊥AC，点E在边AD上，满足=，点F在AB上，满足 =，连结BE和CF相交于点G，则线段CG的长度是     ．

AD为△ABC的中线，G为△ABC的重心，若=2，则=      ．

如图，在△ABC中，E，F分别是AC，BC边上的点，P₁，P₂，P₃，…，P_n−1是AB边的n等分点，CE = AC，CF = BC，∠B = 40°，AB = BC，则∠EP₁F +∠EP₂F +∠EP₃F + … +∠EP _n−1F = ________．