如果三角形的两个内角 α与 β满足 2α+β=90°,那么我们称这样的三角形为“准互余三角形”.
(1)若 ΔABC是“准互余三角形”, ∠C>90°, ∠A=60°,则 ∠B= °;
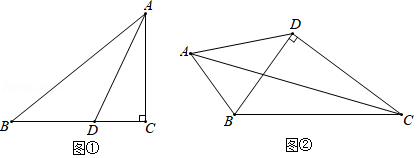
(2)如图①,在 RtΔABC中, ∠ACB=90°, AC=4, BC=5.若 AD是 ∠BAC的平分线,不难证明 ΔABD是“准互余三角形”.试问在边 BC上是否存在点 E(异于点 D),使得 ΔABE也是“准互余三角形”?若存在,请求出 BE的长;若不存在,请说明理由.
(3)如图②,在四边形 ABCD中, AB=7, CD=12, BD⊥CD, ∠ABD=2∠BCD,且 ΔABC是“准互余三角形”,求对角线 AC的长.
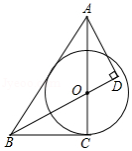
如图,在 ΔABC中, O为 AC上一点,以点 O为圆心, OC为半径做圆,与 BC相切于点 C,过点 A作 AD⊥BO交 BO的延长线于点 D,且 ∠AOD=∠BAD.
(1)求证: AB为 ⊙O的切线;
(2)若 BC=6, tan∠ABC=43,求 AD的长.
如图,在 ΔABC中, AB=8, BC=4, CA=6, CD//AB, BD是 ∠ABC的平分线, BD交 AC于点 E,求 AE的长.

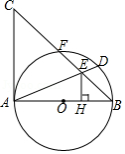
如图,已知 AB为 ⊙O直径, AC是 ⊙O的切线,连接 BC交 ⊙O于点 F,取 ̂BF的中点 D,连接 AD交 BC于点 E,过点 E作 EH⊥AB于 H.
(1)求证: ΔHBE∽;
(2)若 , ,求 和 的长.
若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.

(1)已知 是比例三角形, , ,请直接写出所有满足条件的 的长;
(2)如图1,在四边形 中, ,对角线 平分 , .求证: 是比例三角形.
(3)如图2,在(2)的条件下,当 时,求 的值.
已知在 中, , , , 分别为 , 边上的点(不包括端点),且 ,连接 ,过点 作 ,垂足为点 ,延长 交 于点 .
(1)如图1,过点 作 于点 ,连接 .
①求证:四边形 是平行四边形;
②若 ,求证: ;
(2)如图2,若 ,求 的值.

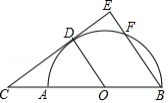
如图, 为半圆 的直径, 为 延长线上一点, 切半圆 于点 ,连接 .作 于点 ,交半圆 于点 .已知 , .
(1)求证: .
(2)求半圆 的半径 的长.
如图,抛物线 与 轴的负半轴交于点 ,与 轴交于点 ,连接 ,点 在抛物线上,直线 与 轴交于点 .
(1)求 的值及直线 的函数表达式;
(2)点 在 轴正半轴上,点 在 轴正半轴上,连接 与直线 交于点 ,连接 并延长交 于点 ,若 为 的中点.
①求证: ;
②设点 的横坐标为 ,求 的长(用含 的代数式表示).

已知正方形 的对角线 , 相交于点 .
(1)如图1, , 分别是 , 上的点, 与 的延长线相交于点 .若 ,求证: ;
(2)如图2, 是 上的点,过点 作 ,交线段 于点 ,连接 交 于点 ,交 于点 .若 ,
①求证: ;
②当 时,求 的长.

如图,在锐角三角形 中,点 , 分别在边 , 上, 于点 , 于点 , .
(1)求证: ;
(2)若 , ,求 的值.

定义:有三个内角相等的四边形叫三等角四边形.
(1)三等角四边形 中, ,求 的取值范围;
(2)如图,折叠平行四边形纸片 ,使顶点 , 分别落在边 , 上的点 , 处,折痕分别为 , .求证:四边形 是三等角四边形.
(3)三等角四边形 中, ,若 ,则当 的长为何值时, 的长最大,其最大值是多少?并求此时对角线 的长.

如图, 为 的直径,弦 ,垂足为点 ,直线 与 的延长线交于点 ,且 .
(1)求证:直线 是 的切线.
(2)若 , ,求线段 的长.

从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
(1)如图1,在 中, 为角平分线, , ,求证: 为 的完美分割线.
(2)在 中, , 是 的完美分割线,且 为等腰三角形,求 的度数.
(3)如图2, 中, , , 是 的完美分割线,且 是以 为底边的等腰三角形,求完美分割线 的长.

试题篮
()