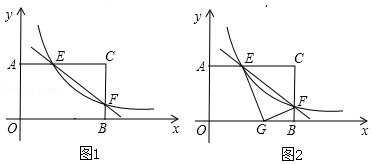
矩形 AOBC中, OB=4, OA=3.分别以 OB, OA所在直线为 x轴, y轴,建立如图1所示的平面直角坐标系. F是 BC边上一个动点(不与 B, C重合),过点 F的反比例函数 y=kx(k>0)的图象与边 AC交于点 E.
(1)当点 F运动到边 BC的中点时,求点 E的坐标;
(2)连接 EF,求 ∠EFC的正切值;
(3)如图2,将 ΔCEF沿 EF折叠,点 C恰好落在边 OB上的点 G处,求此时反比例函数的解析式.
如图,在 RtΔABC中, ∠C=90°, AD平分 ∠BAC交 BC于点 D, O为 AB上一点,经过点 A, D的 ⊙O分别交 AB, AC于点 E, F,连接 OF交 AD于点 G.
(1)求证: BC是 ⊙O的切线;
(2)设 AB=x, AF=y,试用含 x, y的代数式表示线段 AD的长;
(3)若 BE=8, sinB=513,求 DG的长,

在 ΔABC中, AB=AC>BC, D是 BC上一点,连接 AD,作 ΔADE,使 AD=AE,且 ∠DAE=∠BAC,过点 E作 EF//BC交 AB于 F,连接 FC.
(1)如图1.
①连接 BE,求证: ΔAEB≅ΔADC:
②若 D是线段 BC的中点,且 AC=6, BC=4,求 CF的长;
(2)如图2,若点 D在线段 BC的延长线上,且四边形 CDEF是矩形,当 AC=m, BC=n时,求 CD的长(用含 m, n的代数式表示).

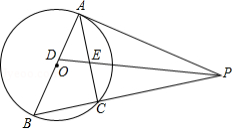
如图, AB是 ⊙O的直径,点 C在 AB的延长线上, AD平分 ∠CAE交 ⊙O于点 D,且 AE⊥CD,垂足为点 E.
(1)求证:直线 CE是 ⊙O的切线.
(2)若 BC=3, CD=3√2,求弦 AD的长.
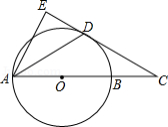
如图, AB是 ⊙O的直径,点 D, E在 ⊙O上, ∠A=2∠BDE,点 C在 AB的延长线上, ∠C=∠ABD.
(1)求证: CE是 ⊙O的切线;
(2)若 BF=2, EF=√13,求 ⊙O的半径长.

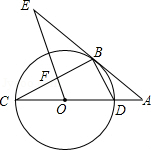
如图, CD是 ⊙O的直径,点 B在 ⊙O上,连接 BC、 BD,直线 AB与 CD的延长线相交于点 A, AB2=AD·AC, OE//BD交直线 AB于点 E, OE与 BC相交于点 F.
(1)求证:直线 AE是 ⊙O的切线;
(2)若 ⊙O的半径为3, cosA=45,求 OF的长.
如图,直线 y1=mx+n(m≠0)与双曲线 y2=kx(k≠0)相交于 A(−1,2)和 B(2,b)两点,与 y轴交于点 C,与 x轴交于点 D.
(1)求 m, n的值;
(2)在 y轴上是否存在一点 P,使 ΔBCP与 ΔOCD相似?若存在求出点 P的坐标;若不存在,请说明理由.

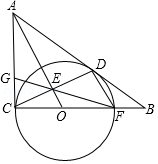
如图, ΔABC中,以 BC为直径的 ⊙O交 AB于点 D, AE平分 ∠BAC交 BC于点 E,交 CD于点 F.且 CE=CF.
(1)求证:直线 CA是 ⊙O的切线;
(2)若 BD=43DC,求 DFCF的值.

如图,在 中,直径
中,直径 垂直于不过圆心
垂直于不过圆心 的弦
的弦 ,垂足为点
,垂足为点 ,连接
,连接 ,点
,点 在
在 上,且
上,且
(1)求证: ;
;
(2)过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点 ,试判断
,试判断 与
与 是否相等,并说明理由;
是否相等,并说明理由;
(3)设 半径为4,点
半径为4,点 为
为 中点,点
中点,点 在
在 上,求线段
上,求线段 的最小值.
的最小值.

如图,在正方形 ABCD中,点 E、 G分别是边 AD、 BC的中点, AF=14AB.
(1)求证: EF⊥AG;
(2)若点 F、 G分别在射线 AB、 BC上同时向右、向上运动,点 G运动速度是点 F运动速度的2倍, EF⊥AG是否成立(只写结果,不需说明理由)?
(3)正方形 ABCD的边长为4, P是正方形 ABCD内一点,当 SΔPAB=SΔOAB,求 ΔPAB周长的最小值.

如图,点 E是正方形 ABCD的边 BC延长线上一点,连接 DE,过顶点 B作 BF⊥DE,垂足为 F, BF分别交 AC于 H,交 CD于 G.
(1)求证: BG=DE;
(2)若点 G为 CD的中点,求 HGGF的值.

如图, ⊙O与 RtΔABC的直角边 AC和斜边 AB分别相切于点 C、 D,与边 BC相交于点 F, OA与 CD相交于点 E,连接 FE并延长交 AC边于点 G.
(1)求证: DF//AO;
(2)若 AC=6, AB=10,求 CG的长.
如图,以 AB为直径的 ⊙O外接于 ΔABC,过 A点的切线 AP与 BC的延长线交于点 P, ∠APB的平分线分别交 AB, AC于点 D, E,其中 AE, BD(AE<BD)的长是一元二次方程 x2−5x+6=0的两个实数根.
(1)求证: PA⋅BD=PB⋅AE;
(2)在线段 BC上是否存在一点 M,使得四边形 ADME是菱形?若存在,请给予证明,并求其面积;若不存在,说明理由.
如图,将矩形 ABCD沿 AF折叠,使点 D落在 BC边上的点 E处,过点 E作 EG//CD交 AF于点 G,连接 DG.
(1)求证:四边形 EFDG是菱形;
(2)探究线段 EG、 GF、 AF之间的数量关系,并说明理由;
(3)若 AG=6, EG=2√5,求 BE的长.

试题篮
()