在矩形ABCD中,对角线AC,BD相交于点O, , ,点E是BC边上一点,直线OE交CD边所在的直线于点F,若 ,则 .
如图,正方形ABCD的边长为 ,对角线AC、BD相交于点O,E是OC的中点,连接BE,过点A作 于点M,交BD于点F,则FM的长为 .

如图,一张三角形纸片ABC,∠C=90°,AC=8cm,BC=6cm.现将纸片折叠:使点A与点B重合,那么折痕长等于 cm.
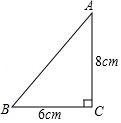
如图,在Rt△ ABC中,∠ ABC=90°, C(0,﹣3), CD=3 AD,点 A在反比例函数 y= 图象上,且 y轴平分∠ ACB,求 k= .
在Rt△ ABC中,∠ C=90°, AD平分∠ CAB, BE平分∠ ABC, AD、 BE相交于点 F,且 AF=4, EF= ,则 AC= .

已知正方形 ABCD的面积是2, E为正方形一边 BC在从 B到 C方向的延长线上的一点,若 CE= ,连接 AE,与正方形另外一边 CD交于点 F,连接 BF并延长,与线段 DE交于点 G,则 BG的长为 .
如图,在Rt△ ABC中,∠ ABC=90°, BC=3, D为斜边 AC的中点,连接 BD,点 F是 BC边上的动点(不与点 B、 C重合),过点 B作 BE⊥ BD交 DF延长线交于点 E,连接 CE,下列结论:
①若 BF= CF,则 CE 2+ AD 2= DE 2;
②若∠ BDE=∠ BAC, AB=4,则 CE= ;
③△ ABD和△ CBE一定相似;
④若∠ A=30°,∠ BCE=90°,则 DE= .
其中正确的是 .(填写所有正确结论的序号)

如图,在平面直角坐标系中,已知 A(﹣1,0), B(0,2),将△ ABO沿直线 AB翻折后得到△ ABC,若反比例函数 y= ( x<0)的图象经过点 C,则 k= .

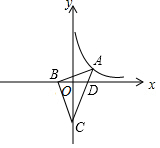
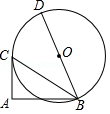
如图, BD是⊙ O的直径, A是⊙ O外一点,点 C在⊙ O上, AC与⊙ O相切于点 C,∠ CAB=90°,若 BD=6, AB=4,∠ ABC=∠ CBD,则弦 BC的长为 .
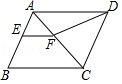
如图, P是▱ ABCD的边 AD上一点, E、 F分别是 PB、 PC的中点,若▱ ABCD的面积为16 cm 2,则△ PEF的面积(阴影部分)是 cm 2.

如图,在Rt△ ACB中,∠ ACB=90°, AC= BC, D是 AB上的一个动点(不与点 A, B重合),连接 CD,将 CD绕点 C顺时针旋转90°得到 CE,连接 DE, DE与 AC相交于点 F,连接 AE.下列结论:
①△ ACE≌△ BCD;
②若∠ BCD=25°,则∠ AED=65°;
③ DE 2=2 CF• CA;
④若 AB=3 , AD=2 BD,则 AF= .
其中正确的结论是 .(填写所有正确结论的序号)

如图,在▱ ABCD中, AC是一条对角线, EF∥ BC,且 EF与 AB相交于点 E,与 AC相交于点 F,3 AE=2 EB,连接 DF.若 S △ AEF=1,则 S △ ADF的值为 .
如图,⊙ O为等腰三角形 ABC的外接圆, AB是⊙ O的直径, AB=12, P为 上任意一点(不与点 B, C重合),直线 CP交 AB的延长线于点 Q,⊙ O在点 P处的切线 PD交 BQ于点 D,则下列结论:①若∠ PAB=30°,则 的长为π;②若 PD∥ BC,则 AP平分∠ CAB;③若 PB= BD,则 PD=6 ;④无论点 P在 上的位置如何变化, CP• CQ=108.其中正确结论的序号为 .

试题篮
()