如图,边长为1的正方形ABCD的对角线AC、BD相交于点O.有直角∠MPN,使直角顶点P与点O重合,直角边PM、PN分别与OA、OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM、PN分别交AB、BC于E、F两点,连接EF交OB于点G,则下列结论中正确的是 .
(1) ;(2) ;(3) ;(4)在旋转过程中,当△BEF与△COF的面积之和最大时, ;(5) .

如图(1),PT与⊙O1相切于点T,PB与⊙O1相交于A、B两点,可证明 ,从而有 .请应用以上结论解决下列问题:如图(2),PAB、PCD分别与⊙O2相交于A、B、C、D四点,已知 ,则CD= .

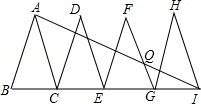
如图,已知△ABC、△DCE、△FEG、△HGI是4个全等的等腰三角形,底边BC、CE、EG、GI在同一直线上,且AB=2,BC=1,连接AI,交FG于点Q,则QI= .
如图,在正方形 ABCD中,点 E, F分别在 BC, CD上,如果 AE=3, EF=2, AF= ,那么正方形 ABCD的边长等于 .

如图,在正方形ABCD中,点E,F分别在BC,CD上,如果AE=3,EF=2,AF= ,那么正方形ABCD的边长等于 .

如图,在Rt△ ABC中,∠ C=90°, AC=3, BC=4,把△ ABC绕 AB边上的点 D顺时针旋转90°得到△ A′ B′ C′, A′ C′交 AB于点 E,若 AD= BE,则△ A′ DE的面积是 .

对于一个矩形ABCD及⊙M给出如下定义:在同一平面内,如果矩形ABCD的四个顶点到⊙M上一点的距离相等,那么称这个矩形ABCD是⊙M的“伴侣矩形”.如图,在平面直角坐标系xOy中,直线l:y= x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .
x﹣3交x轴于点M,⊙M的半径为2,矩形ABCD沿直线运动(BD在直线l上),BD=2,AB∥y轴,当矩形ABCD是⊙M的“伴侣矩形”时,点C的坐标为 .

魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中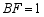 ,
,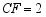 ,则
,则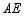 的长为 .
的长为 .
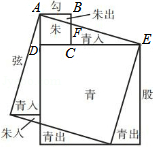
魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中 ,
,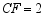 ,则
,则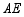 的长为 .
的长为 .

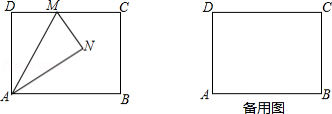
如图,矩形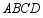 中,
中,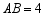 ,
, ,
,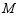 是边
是边 上一点,将
上一点,将 沿直线
沿直线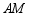 对折,得到
对折,得到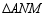 .
.
(1)当 平分
平分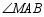 时,求
时,求 的长;
的长;
(2)连接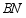 ,当
,当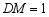 时,求
时,求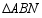 的面积;
的面积;
(3)当射线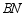 交线段
交线段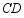 于点
于点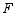 时,求
时,求 的最大值.
的最大值.
试题篮
()