小波在复习时,遇到一个课本上的问题,温故后进行了操作、推理与拓展.
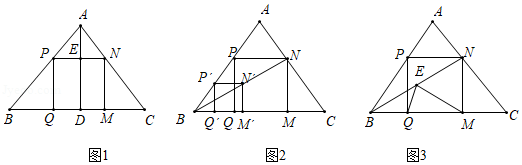
(1)温故:如图1,在中,
于点
,正方形
的边
在
上,顶点
,
分别在
,
上,若
,
,求正方形
的边长.
(2)操作:能画出这类正方形吗?小波按数学家波利亚在《怎样解题》中的方法进行操作:如图2,任意画,在
上任取一点
,画正方形
,使
,
在
边上,
在
内,连结
并延长交
于点
,画
于点
,
交
于点
,
于点
,得到四边形
.小波把线段
称为“波利亚线”.
(3)推理:证明图2中的四边形是正方形.
(4)拓展:在(2)的条件下,在射线上截取
,连结
,
(如图
.当
时,猜想
的度数,并尝试证明.
请帮助小波解决“温故”、“推理”、“拓展”中的问题.
如图,在△ ABC中, AD⊥ BC, BE⊥ AC,垂足分别为 D, E, AD与 BE相交于点 F.
(1)求证:△ ACD∽△ BFD;
(2)当tan∠ ABD=1, AC=3时,求 BF的长.

阅读下面材料:
小明遇到这样一个问题:如图1, 中, ,点 在 边上, , ,垂足为 ,求证: .
小明经探究发现,过点 作 ,垂足为 ,得到 ,从而可证 (如图 ,使问题得到解决.
(1)根据阅读材料回答: 与 全等的条件是 (填“ ”、“ ”、“ ”、“ ”或“ ”中的一个)
参考小明思考问题的方法,解答下列问题:
(2)如图3, 中, , , 为 的中点, 为 的中点,点 在 的延长线上,且 ,若 ,求 的长;
(3)如图4, 中, , ,点 、 分别在 、 边上,且 (其中 , ,求 的值(用含 的式子表示).

如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
已知:如图,在 中, ,点 是斜边 的中点, ,且 , 于点 ,连接 、 .
(1)求证: ;
(2)求证: ;
(3)设 的面积为 ,四边形 的面积为 ,当 时,求 的值.

问题背景 如图(1),已知 ,求证: ;
尝试应用 如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值;
拓展创新 如图(3), 是 内一点, , , , ,直接写出 的长.

如图, ,点 是 平分线上的一点,过点 分别作 , ,垂足分别为点 , , ,点 为线段 上的一点(点 不与点 、 重合),连接 ,以 为直角边,点 为直角顶点,作等腰直角三角形 ,点 落在 左侧.
(1)求证: ;
(2)连接 ,请你判断 与 的位置关系,并说明理由;
(3)设 , 的面积为 ,求 与 之间的函数关系式.

某数学课外活动小组在学习了勾股定理之后,针对图1中所示的“由直角三角形三边向外侧作多边形,它们的面积 , , 之间的关系问题”进行了以下探究:
类比探究
(1)如图2,在 中, 为斜边,分别以 , , 为斜边向外侧作 , , ,若 ,则面积 , , 之间的关系式为 ;
推广验证
(2)如图3,在 中, 为斜边,分别以 , , 为边向外侧作任意 , , ,满足 , ,则(1)中所得关系式是否仍然成立?若成立,请证明你的结论;若不成立,请说明理由;
拓展应用
(3)如图4,在五边形 中, , , , ,点 在 上, , ,求五边形 的面积.

在矩形 中, ,点 是 边上的任意一点(不含 , 两端点),过点 作 ,交对角线 于点 .

(1)如图1,将 沿对角线 翻折得到 , 交 于点 .
求证: 是等腰三角形;
(2)如图2,将 绕点 逆时针方向旋转得到△ ,连接 , .设旋转角为 .
①若 ,即 在 的内部时,求证:△ △ .
②如图3,若点 是 的中点,△ 能否为直角三角形?如果能,试求出此时 的值,如果不能,请说明理由.
如图1,直线 与 轴交于点 ,与 轴交于点 ,点 是线段 上一动点 .以点 为圆心, 长为半径作 交 轴于另一点 ,交线段 于点 ,连接 并延长交 于点 .

(1)求直线 的函数表达式和 的值;
(2)如图2,连接 ,当 时,
①求证: ;
②求点 的坐标;
(3)当点 在线段 上运动时,求 的最大值.
如图,在 中, , ,正方形 的边长为2,将正方形 绕点 旋转一周,连接 、 、 .
(1)请找出图中与 相似的三角形,并说明理由;
(2)求当 、 、 三点在一直线上时 的长;
(3)设 的中点为 ,连接 ,试求 长的取值范围.

已知正方形 中 与 交于 点,点 在线段 上,作直线 交直线 于 ,过 作 于 ,设直线 交 于 .

(1)如图1,当 在线段 上时,求证: ;
(2)如图2,当 在线段 上,连接 ,当 时,求证: ;
(3)在图3,当 在线段 上,连接 ,当 时,求证: .
已知: 、 两点在直线 的同一侧,线段 , 均是直线 的垂线段,且 在 的右边, ,将 沿直线 向右平移,在平移过程中,始终保持 不变, 边与直线 相交于点 .
(1)当 与 重合时(如图2所示),设点 是 的中点,连接 .求证:四边形 是正方形;
(2)请利用如图1所示的情形,求证: ;
(3)若 ,且当 时,请直接写出 和 的长.

试题篮
()