如图, 中, , , , 于点 , 是线段 上一点, , ,连接 、 .设 、 的中点分别为 、 .
(1)求 的长;
(2)求 的长;
(3)设 与 的交点为 ,请直接写出 的值.

在 中, 、 分别为线段 、 上的点(不与 、 、 重合).
(1)如图1,若 ,求证:
(2)如图2,若 不与 平行,(1)中的结论是否仍然成立?请说明理由;
(3)如图3,若 上一点 恰为 的重心, ,求 的值.

在 中, , 是 内一点,连接 , ,在 左侧作 ,使 ,以 和 为邻边作 ,连接 , .

(1)若 , .
①如图1,当 , , 三点共线时, 与 之间的数量关系为 .
②如图2,当 , , 三点不共线时,①中的结论是否仍然成立?请说明理由.
(2)若 , , ,且 , , 三点共线,求 的值.
若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,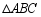 中,设
中,设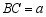 ,
,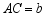 ,
,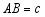 ,各边上的高分别记为
,各边上的高分别记为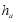 ,
,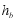 ,
,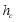 ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为 ,
,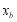 ,
,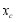
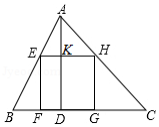
(1)模拟探究:如图,正方形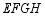 为
为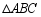 的
的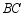 边上的内接正方形,求证:
;
边上的内接正方形,求证:
;
(2)特殊应用:若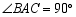 ,
,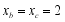 ,求
的值;
,求
的值;
(3)拓展延伸:若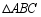 为锐角三角形,
为锐角三角形,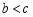 ,请判断
,请判断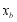 与
与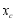 的大小,并说明理由.
的大小,并说明理由.
如图1,在四边形 中,若 平分 , ,且 ,则我们称这样的四边形 为“黄金四边形”, 称为“黄金角”.
【概念理解】(1)已知四边形 为“黄金四边形”, 为“黄金角”, ,若 ,则 .
【问题探究】(2)如图2,在四边形 中, , .求证:四边形 为“黄金四边形”.
【拓展延伸】(3)如图3,在“黄金四边形” 中, 为“黄金角”, ,在四边形 外部依次作△ ,△ , ,使四边形 , , 均为“黄金四边形”,且满足 , ,2, 均为“黄金角”, ,2,
①若 ,则第 个“黄金四边形”中, (用含 的式子表示).
②若“黄金角” ,则当 , , 三点第一次在同一条直线上时, .

在现实生活中,我们经常会看到许多“标准”的矩形,如我们的课本封面、 的打印纸等,其实这些矩形的长与宽之比都为 ,我们不妨就把这样的矩形称为“标准矩形”,在“标准矩形” 中, 为 边上一定点,且 ,如图所示.
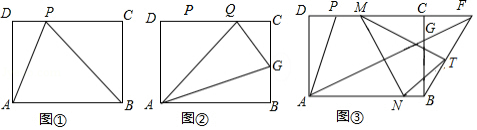
(1)如图①,求证: ;
(2)如图②,点 在 上,且 ,若 为 边上一动点,当 的周长最小时,求 的值;
(3)如图③,已知 ,在(2)的条件下,连接 并延长交 的延长线于点 ,连接 , 为 的中点, 、 分别为线段 与 上的动点,且始终保持 ,请证明: 的面积 为定值,并求出这个定值.
如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
如图,正方形 ABCD的边长为3 cm, P, Q分别从 B, A出发沿 BC, AD方向运动, P点的运动速度是1 cm/秒, Q点的运动速度是2 cm/秒,连接 A, P并过 Q作 QE⊥ AP垂足为 E.
(1)求证:△ ABP∽△ QEA;
(2)当运动时间 t为何值时,△ ABP≌△ QEA;
(3)设△ QEA的面积为 y,用运动时刻 t表示△ QEA的面积 y(不要求考 t的取值范围).(提示:解答(2)(3)时可不分先后)

如图, 是半圆 的直径, 是 延长线上的点, 的垂直平分线交半圆于点 ,交 于点 ,连接 , .已知半圆 的半径为3, .
(1)求 的长.
(2)点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.

问题背景 如图(1),已知 ,求证: ;
尝试应用 如图(2),在 和 中, , , 与 相交于点 ,点 在 边上, ,求 的值;
拓展创新 如图(3), 是 内一点, , , , ,直接写出 的长.

如图,在△ ABC中, AD⊥ BC, BE⊥ AC,垂足分别为 D, E, AD与 BE相交于点 F.
(1)求证:△ ACD∽△ BFD;
(2)当tan∠ ABD=1, AC=3时,求 BF的长.

已知矩形 的一条边 ,将矩形 折叠,使得顶点 落在 边上的 点处
(Ⅰ)如图1,已知折痕与边 交于点 ,连接 、 、 .若 与 的面积比为 ,求边 的长.
(Ⅱ)如图2,在(Ⅰ)的条件下,擦去折痕 、线段 ,连接 .动点 在线段 上(点 与点 、 不重合),动点 在线段 的延长线上,且 ,连接 交 于点 ,作 于点 .试问当动点 、 在移动的过程中,线段 的长度是否发生变化?若变化,说明变化规律.若不变,求出线段 的长度.

已知:如图,在 中, ,点 是斜边 的中点, ,且 , 于点 ,连接 、 .
(1)求证: ;
(2)求证: ;
(3)设 的面积为 ,四边形 的面积为 ,当 时,求 的值.

试题篮
()