如图, 在平面直角坐标系中, 把矩形 沿对角线 所在直线折叠, 点 落在点 处, 与 轴相交于点 ,矩形 的边 , 的长是关于 的一元二次方程 的两个根, 且 .
(1) 求线段 , 的长;
(2) 求证: ,并求出线段 的长;
(3) 直接写出点 的坐标;
(4) 若 是直线 上一个动点, 在坐标平面内是否存在点 ,使以点 , , , 为顶点的四边形是菱形?若存在, 请直接写出 点的坐标;若不存在, 请说明理由 .

如图, 是半圆 的直径, 是 延长线上的点, 的垂直平分线交半圆于点 ,交 于点 ,连接 , .已知半圆 的半径为3, .
(1)求 的长.
(2)点 是线段 上一动点,连接 ,作 , 交线段 于点 .当 为等腰三角形时,求 的长.

如图1,在正方形 中,点 是 边上的一个动点(点 与点 , 不重合),连接 ,过点 作 于点 ,交 于点 .
(1)求证: ;
(2)如图2,当点 运动到 中点时,连接 ,求证: ;
(3)如图3,在(2)的条件下,过点 作 于点 ,分别交 , 于点 , ,求 的值.

如图,在边长为4的正方形 中, 是 边上一动点(不含 、 两点),将 沿直线 翻折,点 落在点 处;在 上有一点 ,使得将 沿直线 翻折后,点 落在直线 上的点 处,直线 交 于点 ,连接 , .则以下结论中正确的有 (写出所有正确结论的序号)
① ;
②四边形 的面积最大值为10;
③当 为 中点时, 为线段 的中垂线;
④线段 的最小值为 ;
⑤当 时, .

已知正方形 的边长为1,点 为正方形内一动点,若点 在 上,且满足 ,延长 交 于点 ,连接 .
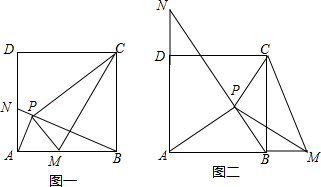
(1)如图一,若点 在线段 上,求证: ; ;
(2)①如图二,在点 运动过程中,满足 的点 在 的延长线上时, 和 是否成立?(不需说明理由)
②是否存在满足条件的点 ,使得 ?请说明理由.
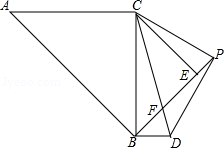
如图, 和 均为等腰直角三角形,且 , ,点 为线段 延长线上一点,连接 以 为直角边向下作等腰直角 ,线段 与 相交于点
(1)求证: ;
(2)连接 ,请你判断 与 有什么位置关系?并说明理由;
(3)设 , 的面积为 ,求 与 之间的函数关系式.
如图,在△ ABC中, AD⊥ BC, BE⊥ AC,垂足分别为 D, E, AD与 BE相交于点 F.
(1)求证:△ ACD∽△ BFD;
(2)当tan∠ ABD=1, AC=3时,求 BF的长.

在△ABC中, ,D是△ABC内部或BC边上的一个动点(与B、C不重合),以D为顶点作△DEF,使△DEF∽△ABC(相似比k>1),EF∥BC.
(1)求∠D的度数;
(2)若两三角形重叠部分的形状始终是四边形AGDH.
①如图1,连接GH、AD,当 时,请判断四边形AGDH的形状,并证明;
②当AGDH的面积最大时,过A作
于P,且
,求k的值.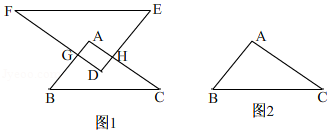
如图,在平面直角坐标系中,已知 A(﹣3,﹣2), B(0,﹣2), C(﹣3,0), M是线段 AB上的一个动点,连接 CM,过点 M作 MN⊥ MC交 y轴于点 N,若点 M、 N在直线 y= kx+ b上,则 b的最大值是( )

| A. |
﹣ |
B. |
﹣ |
C. |
﹣1 |
D. |
0 |
如图,在矩形 ABCD中, AB=3, BC=5, E是 AD上的一个动点. 
(1)如图1,连接 BD, O是对角线 BD的中点,连接 OE.当 OE= DE时,求 AE的长;
(2)如图2,连接 BE, EC,过点 E作 EF⊥ EC交 AB于点 F,连接 CF,与 BE交于点 G.当 BE平分∠ ABC时,求 BG的长;
(3)如图3,连接 EC,点 H在 CD上,将矩形 ABCD沿直线 EH折叠,折叠后点 D落在 EC上的点 D'处,过点 D′作 D′ N⊥ AD于点 N,与 EH交于点 M,且 AE=1.
①求 的值;
②连接 BE,△ D' MH与△ CBE是否相似?请说明理由.
如图,正方形 ABCD的边长为3 cm, P, Q分别从 B, A出发沿 BC, AD方向运动, P点的运动速度是1 cm/秒, Q点的运动速度是2 cm/秒,连接 A, P并过 Q作 QE⊥ AP垂足为 E.
(1)求证:△ ABP∽△ QEA;
(2)当运动时间 t为何值时,△ ABP≌△ QEA;
(3)设△ QEA的面积为 y,用运动时刻 t表示△ QEA的面积 y(不要求考 t的取值范围).(提示:解答(2)(3)时可不分先后)

若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形, 中,设
中,设 ,
, ,
, ,各边上的高分别记为
,各边上的高分别记为 ,
, ,
, ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为 ,
, ,
,
(1)模拟探究:如图,正方形 为
为 的
的 边上的内接正方形,求证:
;
边上的内接正方形,求证:
;
(2)特殊应用:若 ,
, ,求
的值;
,求
的值;
(3)拓展延伸:若 为锐角三角形,
为锐角三角形, ,请判断
,请判断 与
与 的大小,并说明理由.
的大小,并说明理由.

若正方形有两个相邻顶点在三角形的同一条边上,其余两个顶点分别在三角形的另两条边上,则正方形称为三角形该边上的内接正方形,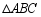 中,设
中,设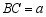 ,
,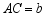 ,
,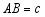 ,各边上的高分别记为
,各边上的高分别记为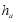 ,
,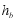 ,
,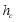 ,各边上的内接正方形的边长分别记为
,各边上的内接正方形的边长分别记为 ,
,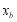 ,
,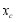
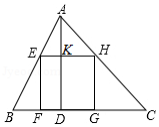
(1)模拟探究:如图,正方形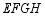 为
为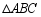 的
的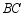 边上的内接正方形,求证:
;
边上的内接正方形,求证:
;
(2)特殊应用:若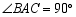 ,
,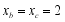 ,求
的值;
,求
的值;
(3)拓展延伸:若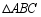 为锐角三角形,
为锐角三角形,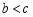 ,请判断
,请判断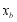 与
与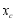 的大小,并说明理由.
的大小,并说明理由.
如图, ,正方形 ,正方形 ,正方形 ,正方形 , ,的顶点 , , , , ,在射线 上,顶点 , , , , , ,在射线 上,连接 交 于点 ,连接 交 于点 ,连接 交 于点 , ,连接 交 于点 ,连接 交 于点 , ,按照这个规律进行下去,设 与△ 的面积之和为 ,△ 与△ 的面积之和为 ,△ 与△ 的面积之和为 , ,若 ,则 等于 .(用含有正整数 的式子表示)

试题篮
()