问题探究:
小红遇到这样一个问题:如图1, 中, , , 是中线,求 的取值范围.她的做法是:延长 到 ,使 ,连接 ,证明 ,经过推理和计算使问题得到解决.
请回答:(1)小红证明 的判定定理是: ;
(2) 的取值范围是 ;
方法运用:
(3)如图2, 是 的中线,在 上取一点 ,连结 并延长交 于点 ,使 ,求证: .
(4)如图3,在矩形 中, ,在 上取一点 ,以 为斜边作 ,且 ,点 是 的中点,连接 , ,求证: .

如图,在中,
,
,
,
平分
,
交
于点
,
交
于点
,
的外接圆
交
于点
,连接
.
(1)求证:是
的切线;
(2)求的半径
及
的正切值.
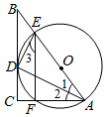
如图,在平行四边形 中, ,垂足为点 ,以 为直径的 与边 相切于点 ,连接 交 于点 ,连接 .
(1)求证: .
(2)若 ,求 的值.
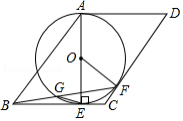
如图,为
的直径,
为
上的一点,
,
,
的延长线交
于点
,连接
.
(1)求证:是
的切线;
(2)若为
的中点,求
的值.

已知点 为正方形 的边 上一点,连接 ,过点 作 ,垂足为 ,交 于点 .
(1)求证: ;
(2)若 为 的中点,求 .

如图,四边形 内接于 , , ,垂足为 ,点 在 的延长线上,且 ,连接 、 .
(1)求证: ;
(2)若 , ,求 的值.

已知在平面直角坐标系中(如图),已知抛物线
经过点
,对称轴是直线
,顶点为
.
(1)求这条抛物线的表达式和点的坐标;
(2)点在对称轴上,且位于顶点上方,设它的纵坐标为
,联结
,用含
的代数式表示
的余切值;
(3)将该抛物线向上或向下平移,使得新抛物线的顶点在
轴上.原抛物线上一点
平移后的对应点为点
,如果
,求点
的坐标.
如图,为
的直径,
为
上的一点,
,
,
的延长线交
于点
,连接
.
(1)求证:是
的切线;
(2)若为
的中点,求
的值.
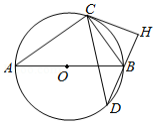
如图, 为圆 的直径, 为圆 上一点, 为 延长线一点,且 , 于点 .
(1)求证:直线 为圆 的切线;
(2)设 与圆 交于点 , 的延长线与 交于点 ,已知 , , ,求 的值.

如图,根据图中数据解答下列问题.
(1)sin2A1+sin2B1=________;
sin2A2+sin2B2=________;
sin2A3+sin2B3=________.
观察上述等式,猜想:在Rt△ABC中,∠C=90°,都有sin2A+sin2B=________.
(2)如图④,在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别是a,b,c,利用三角函数的定义和勾股定理,证明(1)中的猜想.
(3)已知∠A+∠B=90°,且 ,求sinB.
,求sinB.
如图,在菱形 中,对角线 与 相交于点 , , ,点 在边 上, ,连结 交 于点 .
(1)求 的长.
(2) 的值为 .

如图,已知 的顶点坐标分别为 , , .动点 , 同时从 点出发, 沿 , 沿折线 ,均以每秒1个单位长度的速度移动,当一个动点到达终点 时,另一个动点也随之停止移动,移动的时间记为 秒.连接 .
(1)求直线 的解析式;
(2)移动过程中,将 沿直线 翻折,点 恰好落在 边上点 处,求此时 值及点 的坐标;
(3)当点 , 移动时,记 在直线 右侧部分的面积为 ,求 关于时间 的函数关系式.

如图,在 和 的斜边分别为正方形的边 和 ,其中 .
(1)求证: ;
(2)线段 与线段 相交于 ,若 ,求 的值.

试题篮
()