如图,一艘轮船以40海里/时的速度在海面上航行,当它行驶到A处时, 发现它的北偏东30°方向有一灯塔B。轮船继续向北航行2小时后到达C处,发现灯塔B在它的北偏东60°方向。若轮船继续向北航行,那么当再过多长时间时轮船离灯塔最近?( )
A.1小时 B. 小时 C.2小时 D.
小时 C.2小时 D. 小时
小时
如图,将三角板的直角顶点放置在直线AB上的点O处.使斜边CD∥AB,则∠a的余弦值为__________.
王师傅在楼顶上的点A出测得楼前一棵树CD的顶端C的俯角为60。。,又知水平距离BD=10cm,楼高AB=24cm,则树高CD为( )。
A.(24-10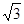 )m )m |
B.(24-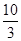 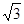 m m |
C.(24-5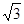 )m )m |
D.9m |
如图,小昆家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在他家北偏东60度400m处,那么水塔所在的位置到公路的距离AB是 m.


如果∠A为锐角,cosA= ,那么∠A 取值范围是 ( )
,那么∠A 取值范围是 ( )
| A.0°< ∠A≤30° | B.30°< ∠A≤45° | C.45°<∠A ≤60° | D.60°< ∠A < 90° |
如图,先锋村准备在坡角为α的山坡上栽树,要求相邻两树之间的水平距离为5米,那么这两树在坡面上的距离AB为( )
A. |
B.5cosα | C. |
D.5sinα |
如图,为了测量山高AC,在水平面B处测得山顶A的仰角是( )
| A.∠A | B.∠ABC | C.∠ABD | D.以上都不对 |
(本题8分)水坝的横断面为梯形ABCD,迎水坡BC的坡角B为30°,背水坡AD坡比为1:1.5,坝顶宽DC=2米,坝高4米,求:
(1)坝底AB的长;
(2)迎水坡BC的坡比.
(本题6分)(1)计算: 4cos245°-|-2| + tan45°;
(2)分解因式:

在Rt△ABC中,∠C=90°,AB=5,AC=2,则cosA的值是( )
A. |
B. |
C. |
D. |
某风景区的湖心岛靠水边有一凉亭A,其正东方向的湖边B处有一棵大树,游客李先生必须在10分钟之内从湖心岛凉亭A处划船赶回湖边B,否则
他将赶不上旅游车约定的发车时间.已知湖边建筑物C在凉亭A的南偏东45°方向上,也在大树B的南偏西32°的方向上,且量得B、C间的距离为100m.若
李先生立即登船以15m/s的速度划行,问他能否在规定时间内赶到B处?
(参考数据:sin32°=0.5299 cos32°=0.8480)
试题篮
()