△ABC中,∠C=90°,点D在边AB上,AD=AC=7,BD= BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
BC.动点M从点C出发,以每秒1个单位的速度沿CA向点A运动,同时,动点N从点D出发,以每秒2个单位的速度沿DA向点A运动.当一个点到达点A时,点M、N两点同时停止运动.设M、N运动的时间为t秒.
⑴ 求cosA的值.
⑵ 当以MN为直径的圆与△ABC一边相切时,求t的值.
如图14-1,在锐角△ABC中,AB = 5,AC = ,∠ACB = 45°.
,∠ACB = 45°.
计算:求BC的长;
操作:将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.如图14-2,当点C1在线段CA的延长线上时.
(1)证明:A1C1⊥CC1;
(2)求四边形A1BCC1的面积;



探究:
将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.连结AA1,CC1,如图14-3.若△ABA1的面积为5,求点C到BC1的距离;
拓展:
将图14-1中的△ABC绕点B按逆时针方向旋转,得到△A1BC1.点E为线段AB中点,点P是线段AC上的动点,在△ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P1,如图14-4.
(1)若点P是线段AC的中点,求线段EP1长度的最大值与最小值;
(2)若点P是线段AC上的任一点,直接写出线段EP1长度的最大值与最小值.
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t( )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.
如图,扇形OAB的半径为4,圆心角∠AOB=90°,点C是 上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
上异于点A、B的一动点,过点C作CD⊥OB于点D,作CE⊥OA于点E,联结DE,过O点作OF⊥DE于点F,点M为线段OD上一动点,联结MF,过点F作NF⊥MF,交OA于点N.
(1)当 时,求
时,求 的值;
的值;
(2)设OM=x,ON=y,当 时,求y关于x 的函数解析式,并写出它的定义域;
时,求y关于x 的函数解析式,并写出它的定义域;
(3)在(2)的条件下,联结CF,当△ECF与△OFN相似时,求OD的长.
如图,正方形ABCD的边长为8,E、F分别为BC、CD边上的点,且tan∠EAF= ,FG∥BC交AE于点G,若FG=5,则EF的长为
,FG∥BC交AE于点G,若FG=5,则EF的长为 
已知:在梯形ABCD中,CD∥AB,AD=DC=BC=2,AB=4.点M从A开始,以每秒1个单位的速度向点B运动;点N从点C出发,沿C→D→A方向,以每秒1个单位的速度向点A运动,若M、N同时出发,其中一点到达终点时,另一个点也停止运动.运动时间为t秒,过点N作NQ⊥CD交AC于点Q.
(1)设△AMQ的面积为S,求S与t的函数关系式,并写出t的取值范围.
(2)在梯形ABCD的对称轴上是否存在点P,使△PAD为直角三角形?若存在,求点P到AB的距离;若不存在,说明理由.
(3)在点M、N运动过程中,是否存在t值,使△AMQ为等腰三角形?若存在,求出t值;若不存在,说明理由.
已知在平面直角坐标系xoy中,二次函数y=-2x²+bx+c的图像经过点A(-3,0)和点B(0,6)。(1)求此二次函数的解析式;(2)将这个二次函数的图像向右平移5个单位后的顶点设为C,直线BC与x轴相交于点D,求∠sin∠ABD;(3)在第(2)小题的条件下,连接OC,试探究直线AB与OC的位置关系,并且说明理由。
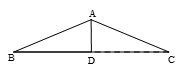
如图,已知等腰△ABC,AD是底边BC上的高,AD:DC=1:3,将△ADC绕着点D旋转,得△DEF,点A、C分别与点E、F对应,且EF与直线AB重合,设AC与DF相交于点O,则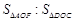 = .
= .
阅读下面材料:
小明遇到这样一个问题:如图1,在边长为 的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)
的正方形ABCD各边上分别截取AE=BF=CG=DH=1,当∠AFQ=∠BGM=∠CHN=∠DEP=45°时,求正方形MNPQ的面积.小明发现:分别延长QE,MF,NG,PH,交FA,GB,HC,ED的延长线于点R,S,T,W,可得△RQF,△SMG,△TNH,△WPE是四个全等的等腰直角三角形(如图2)

请回答:
(1)若将上述四个等腰直角三角形拼成一个新的正方形(无缝隙,不重叠),则这个新的正方形的边长为__________;
(2)求正方形MNPQ的面积.
参考小明思考问题的方法,解决问题:
如图3,在等边△ABC各边上分别截取AD=BE=CF,再分别过点D,E,F作BC,AC,AB的垂线,得到等边△RPQ,若 ,则AD的长为__________.
,则AD的长为__________.
四边形 中,
中, ∥
∥ ,
, ,
, ,
, .点
.点 为射线
为射线 上动点(不与点
上动点(不与点 、
、 重合),点
重合),点 在直线
在直线 上,且
上,且 .记
.记 ,
, ,
, ,
, .
.
(1)当点 在线段
在线段 上时,写出并证明
上时,写出并证明 与
与 的数量关系;
的数量关系;
(2)随着点 的运动,(1)中得到的关于
的运动,(1)中得到的关于 与
与 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的 的取值范围;
的取值范围;
(3)若cos =
= ,试用
,试用 的代数式表示
的代数式表示 .
.
在 中,
中, ,
, ,
, ,⊙
,⊙ 的半径长为1,⊙
的半径长为1,⊙ 交边
交边 于点
于点 ,
,
点 是边
是边 上的动点.
上的动点.
(1)如图1,将⊙ 绕点
绕点 旋转
旋转 得到⊙
得到⊙ ,请判断⊙
,请判断⊙ 与直线
与直线 的位置关系;
的位置关系;
(2)如图2,在(1)的条件下,当 是等腰三角形时,求
是等腰三角形时,求 的长;
的长;
(3)如图3,点 是边
是边 上的动点,如果以
上的动点,如果以 为半径的⊙
为半径的⊙ 和以
和以 为半径的⊙
为半径的⊙ 外切,设
外切,设 ,
, ,求
,求 关于
关于 的函数关系式及定义域..
的函数关系式及定义域..
某住宅小区的物业管理部门为解决住户停车困难,将一条道路辟为停车场,停车位置如图所示。已知矩形ABCD是供一辆机动车停放的车位,其中AB=5.4米,BC=2.2米,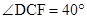 。请计算停车位所占道路的宽度EF(结果精确到0.1米)。
。请计算停车位所占道路的宽度EF(结果精确到0.1米)。
参考数据:sin40°≈0.64 cos40°≈0.77 tan40°≈0.84 
如图(1),在□ABCD中,P是CD边上的一点,AP与BP分别平分∠DAB和∠CBA。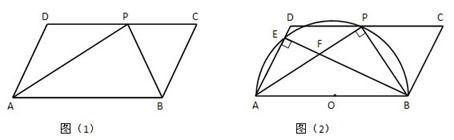
判断△APB是什么三角形?证明你的结论;
比较DP与PC的大小;
如图(2)以AB为直径作半圆O,交AD于点E,连结BE与AP交于点F,若AD=5cm,AP=8cm,求证△AEF∽△APB,并求tan∠AFE的值。
如图,在直角梯形ABCD中,∠D=∠BCD=90°,∠B=60°, AB=6,AD=9,
点E是CD上的一个动点(E不与D重合),过点E作EF∥AC,交AD于点F(当E运
动到C时,EF与AC重合巫台).把△DEF沿EF对折,点D的对应点是点G,设DE=x,
△GEF与梯形ABCD重叠部分的面积为y。
(1) 求CD的长及∠1的度数;
(2) 若点G恰好在BC上,求此时x的值;
(3) 求y与x之间的函数关系式。并求x为何值时,y的值最大?最大值是多少?
试题篮
()