如图是一种儿童的游乐设施﹣儿童荡板.小明想验证这个荡板上方的四边形是否是平行四边形,现在手头只有一根足够长的绳子,请你帮助他设计一个验证方案,并说明理由.
如图,一艘海轮位于灯塔P的北偏东53°方向,距离灯塔100海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东45°方向上的B处.
(1)在图中画出点B,并求出B处与灯塔P的距离(结果取整数);
(2)用方向和距离描述灯塔P相对于B处的位置.
(参考数据:sin53°=0.80,cos53°=0.60,tan53°=0.33, =1.41)
=1.41)
(1)计算:|- |+(-
|+(- )-1-2sin45°+(
)-1-2sin45°+( )0
)0
(2)先化简,再求值:( )÷
)÷ ,其中a=
,其中a= .
.
如图,某塔观光层的最外沿点E为蹦极项目的起跳点.已知点E离塔的中轴线AB的距离OE为10米,塔高AB为123米(AB垂直地面BC),在地面C处测得点E的仰角α=45°,从点C沿CB方向前行40米到达D点,在D处测得塔尖A的仰角β=60°,求点E离地面的高度EF.(结果精确到1米,参考数据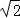 ≈1.4,
≈1.4,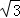 ≈1.7)
≈1.7)
请阅读下列材料:
问题:如图(1),圆柱的底面半径为4cm,圆柱高AB为2cm,BC是底面直径,求一只蚂蚁从点A出发沿圆柱表面爬行到点C的最短路线,小明设计了两条路线:
路线1:高线AB+底面直径BC,如图(1)所示.
路线2:侧面展开图中的线段AC,如图(2)所示.
设路线1的长度为l1,则l1=AB+BC=2+8=10;
设路线2的长度为l2,则l2= =
= =
= ;
;
∵ =102﹣(4+16π2)=96﹣16π2=16(6﹣π2)<0
=102﹣(4+16π2)=96﹣16π2=16(6﹣π2)<0
∴ 即l1<l2
即l1<l2
所以选择路线1较短.
(1)小明对上述结论有些疑惑,于是他把条件改成:“圆柱的底面半径为2cm,高AB为4cm”继续按前面的路线进行计算.(结果保留π)
①此时,路线1:l1= .路线2:l2= .
②所以选择哪条路线较短?试说明理由.
(2)请你帮小明继续研究:当圆柱的底面半径为2cm,高为hcm时,应如何选择上面的两条路线才能使蚂蚁从点A出发沿圆柱表面爬行到点C的路线最短.
为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ≈1.41,
≈1.41, ≈1.73,结果保留整数)
≈1.73,结果保留整数)
如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°相距20海里的C处救生船,并通知救生船,遇险船在它的正东方向B处,现救生船沿着航线CB前往B处救援,若救生船的速度为20海里/时,请问:救生船到达B处大约需要多长时间?(结果精确到0.1小时:参考数据:sin38°≈0.62,cos38°≈0.79,sin22°≈0.37,cos22°≈0.93,sin37°≈0.60,cos37°≈0.80)
(1)计算:2014﹣(﹣1)2014+ ﹣|﹣3
﹣|﹣3 |
|
(2)先化简,再求值: ﹣
﹣ ÷
÷ ,其中x=4cos60°+1.
,其中x=4cos60°+1.
(本小题满分6分)如图,有两棵树,一棵高10米,另一棵高4米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,求小鸟至少飞行的距离.
试题篮
()