. 如图:某片绿地的形状如图所示,其中∠A=60º,AB⊥BC,AD⊥CD,AB=200米,CD=100米,求AD、BC的长(精确到1米, ≈1.73
≈1.73
.如图,已知:在△ABC中,∠A=60 ,∠B=45
,∠B=45 ,AB=8.求△ABC的面积(结果可保留根号)。
,AB=8.求△ABC的面积(结果可保留根号)。
、已知:如图,在ΔABC中,∠ACB=90°,CD⊥AB,垂足为D,若∠B=30°,CD=6,求AB的长.
已知:如图,在矩形 中,点
中,点 在对角线
在对角线 上,以
上,以 的长为半径的⊙
的长为半径的⊙ 与
与 ,
, 分别交于点E、点F,且∠
分别交于点E、点F,且∠ =∠
=∠ .
.
(1)判断直线 与⊙
与⊙ 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若 ,
, ,求⊙
,求⊙ 的半径.
的半径.
已知:如图,等边△ABC中,点D为BC边的中点,点F是AB边上一点,点E在线段DF的延长线上,∠BAE=∠BDF,点M在线段DF上,∠ABE=∠DBM.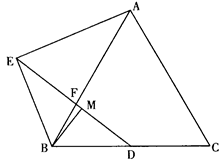
(1)猜想:线段AE、MD之间有怎样的数量关系,并加以证明;
(2)在(1)的条件下延长BM到P,使MP=BM,连接CP,若AB=7 ,AE=
,AE= ,
,
求tan∠BCP的值.
已知:如图,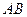 是
是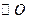 的直径,
的直径,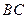 切
切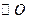 于
于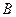 ,
,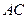 交
交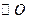 于
于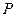 ,
, 为
为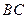 边的中点,连结
边的中点,连结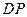 .
.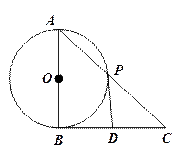
(1) 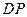 是
是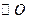 的切线;
的切线;
(2) 若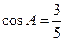 ,
, 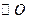 的半径为5, 求
的半径为5, 求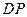 的长.
的长.
如图,A、B是两座现代化城市,C是一个古城遗址,C城在A城的北偏东30°方向,在B城的北偏西45°方向,且C城与A城相距120千米,B城在A城的正东方向,以C为圆心,以60千米为半径的圆形区域内有古迹和地下文物,现要在A、B两城市间修建一条笔直的高速公路,(14')
(1)请你计算公路的长度。(结果保留根号)
(2)请你分析这条公路有没有可能是对古迹或文物赞成损毁。
如图,小明在楼上点A处观察旗杆BC,测得旗杆顶部B的仰角为30°,测得旗杆底部C的俯角为60°,已知点A距地面高AD为12m,求旗杆的高度。(12')
如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE,
(1)求证:△ABE≌△DFA。
(2)如果AD=10,AB=6,求sin∠EDF的值。
如图,在Rt△ABC中,∠C=90°,CD⊥AB于D,已知sinA= ,BD=2,求BC的长。
,BD=2,求BC的长。
计算。(10')
(1)2cos30°-tan60°+tan45°
(2)2sin60°-3tan30°+ (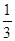 )
)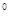 +(-1)
+(-1) 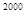
扶沟新开发区供水工程设计从M到N的一段的路线图如图所示,测得N点位于M点南偏东30º,A点位于M点南偏东60º,以A点为中心,半径为500m的圆形区域为文物保护区,又在B点测得BA的方向为南偏东75º,量得MB=400m,请计算后回答:输水路线是否会穿过文物保护区?
试题篮
()