如图,已知 、 是 上两点, 外角的平分线交 于另一点 , 交 的延长线于 .
(1)求证: 是 的切线;
(2) 为 的中点, 为 上一点, 交 于 ,若 , , ,求 的半径.

如图,若 内一点 满足 ,则称点 为 的布罗卡尔点,三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现,后来被数学爱好者法国军官布罗卡尔重新发现,并用他的名字命名,布罗卡尔点的再次发现,引发了研究“三角形几何”的热潮.已知 中, , , 为 的布罗卡尔点,若 ,则 .

如图 是 的直径, 与 相切于点 , 与 相交于点 , 为 上的一点,分别连接 、 , .
(1)求 的度数;
(2)若 ,求 的长度.

如图,矩形 的四个顶点分别在矩形 的各条边上, , , .有以下四个结论:① ;② ;③ ;④矩形 的面积是 .其中一定成立的是 .(把所有正确结论的序号填在横线上)

问题情境:
在综合与实践课上,老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1,将:矩形纸片 沿对角线 剪开,得到 和 .并且量得 , .
操作发现:
(1)将图1中的 以点 为旋转中心,按逆时针方向旋转 ,使 ,得到如图2所示的△ ,过点 作 的平行线,与 的延长线交于点 ,则四边形 的形状是 .
(2)创新小组将图1中的 以点 为旋转中心,按逆时针方向旋转,使 、 、 三点在同一条直线上,得到如图3所示的△ ,连接 ,取 的中点 ,连接 并延长至点 ,使 ,连接 、 ,得到四边形 ,发现它是正方形,请你证明这个结论.
实践探究:
(3)缜密小组在创新小组发现结论的基础上,进行如下操作:将 沿着 方向平移,使点 与点 重合,此时 点平移至 点, 与 相交于点 ,如图4所示,连接 ,试求 的值.

关于 的方程 有两个相等的实数根,其中 是锐角三角形 的一个内角.
(1)求 的值;
(2)若关于 的方程 的两个根恰好是 的两边长,求 的周长.
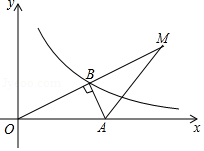
如图①,在平面直角坐标系中,圆心为 的动圆经过点 且与 轴相切于点 .
(1)当 时,求 的半径;
(2)求 关于 的函数解析式,请判断此函数图象的形状,并在图②中画出此函数的图象;
(3)请类比圆的定义(圆可以看成是到定点的距离等于定长的所有点的集合),给(2)中所得函数图象进行定义:此函数图象可以看成是到 的距离等于到 的距离的所有点的集合.
(4)当 的半径为1时,若 与以上(2)中所得函数图象相交于点 、 ,其中交点 在点 的右侧,请利用图②,求 的大小.

如图, 为半圆 的直径, 是 的一条弦, 为 的中点,作 ,交 的延长线于点 ,连接 .
(1)求证: 为半圆 的切线;
(2)若 ,求阴影区域的面积.(结果保留根号和
如图,在平面直角坐标系中, 的斜边 在 轴的正半轴上, ,且 , ,反比例函数 的图象经过点 .
(1)求反比例函数的表达式;
(2)若 与 关于直线 对称,一次函数 的图象过点 、 ,求一次函数的表达式.
在平面直角坐标系中,如果点 坐标为 ,向量 可以用点 的坐标表示为 .
已知: , , , ,如果 ,那么 与 互相垂直,下列四组向量:
① , ;
② , ;
③ , , , ;
④ , , .
其中互相垂直的是 (填上所有正确答案的符号).
试题篮
()