初中数学解直角三角形的应用试题

如图，为了测量河对岸两点 $A$ ， $B$ 之间的距离，在河岸这边取点 $C$ ， $D$ ．测得 $\mathit{CD}=80m$ ， $\angle \mathit{ACD}=90°$ ， $\angle \mathit{BCD}=45°$ ， $\angle \mathit{ADC}=19°17\text{'}$ ， $\angle \mathit{BDC}=56°19\text{'}$ ．设 $A$ ， $B$ ， $C$ ， $D$ 在同一平面内，求 $A$ ， $B$ 两点之间的距离．

（参考数据： $\tan 19°17\text{'}\approx 0.35$ ， $\tan 56°19\text{'}\approx 1.50$ ． $)$

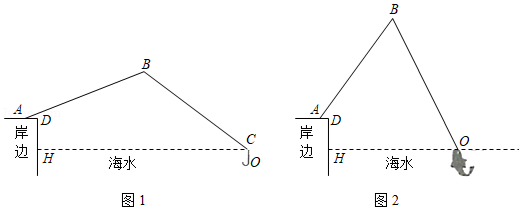
我市的前三岛是众多海钓人的梦想之地．小明的爸爸周末去前三岛钓鱼，将鱼竿 $\mathit{AB}$ 摆成如图1所示．已知 $\mathit{AB}=4.8m$ ，鱼竿尾端 $A$ 离岸边 $0.4m$ ，即 $\mathit{AD}=0.4m$ ．海面与地面 $\mathit{AD}$ 平行且相距 $1.2m$ ，即 $\mathit{DH}=1.2m$ ．

（1）如图1，在无鱼上钩时，海面上方的鱼线 $\mathit{BC}$ 与海面 $\mathit{HC}$ 的夹角 $\angle \mathit{BCH}=37°$ ，海面下方的鱼线 $\mathit{CO}$ 与海面 $\mathit{HC}$ 垂直，鱼竿 $\mathit{AB}$ 与地面 $\mathit{AD}$ 的夹角 $\angle \mathit{BAD}=22°$ ．求点 $O$ 到岸边 $\mathit{DH}$ 的距离；

（2）如图2，在有鱼上钩时，鱼竿与地面的夹角 $\angle \mathit{BAD}=53°$ ，此时鱼线被拉直，鱼线 $\mathit{BO}=5.46m$ ，点 $O$ 恰好位于海面．求点 $O$ 到岸边 $\mathit{DH}$ 的距离．

（参考数据： $\sin 37°=\cos 53°\approx \frac{3}{5}$ ， $\cos 37°=\sin 53°\approx \frac{4}{5}$ ， $\tan 37°\approx \frac{3}{4}$ ， $\sin 22°\approx \frac{3}{8}$ ， $\cos 22°\approx \frac{15}{16}$ ， $\tan 22°\approx \frac{2}{5})$

某限高曲臂道路闸口如图所示， $\mathit{AB}$ 垂直地面 $l_1$ 于点 $A$ ， $\mathit{BE}$ 与水平线 $l_2$ 的夹角为 $\alpha (0°⩽\alpha ⩽90°)$ ， $\mathit{EF}//l_1//l_2$ ，若 $\mathit{AB}=1.4$ 米， $\mathit{BE}=2$ 米，车辆的高度为 $h$ （单位：米），不考虑闸口与车辆的宽度：

①当 $\alpha =90°$ 时， $h$ 小于3.3米的车辆均可以通过该闸口；

②当 $\alpha =45°$ 时， $h$ 等于2.9米的车辆不可以通过该闸口；

③当 $\alpha =60°$ 时， $h$ 等于3.1米的车辆不可以通过该闸口．

则上述说法正确的个数为 $($ 　　 $)$

A．

0个

B．

1个

C．

2个

D．

3个

已知锐角 $\mathit{\Delta ABC}$ 中，角 $A$ 、 $B$ 、 $C$ 的对边分别为 $a$ 、 $b$ 、 $c$ ，边角总满足关系式： $\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}$ ．

（1）如图1，若 $a=6$ ， $\angle B=45°$ ， $\angle C=75°$ ，求 $b$ 的值；

（2）某公园准备在园内一个锐角三角形水池 $\mathit{ABC}$ 中建一座小型景观桥 $\mathit{CD}$ （如图2所示），若 $\mathit{CD}\perp \mathit{AB}$ ， $\mathit{AC}=14$ 米， $\mathit{AB}=10$ 米， $\sin \angle \mathit{ACB}=\frac{5\sqrt{3}}{14}$ ，求景观桥 $\mathit{CD}$ 的长度．

高速公路上有一种标线叫纵向减速标线，外号叫鱼骨线，作用是为了提醒驾驶员在开车时减速慢行．如图，用平行四边形 $\mathit{ABCD}$ 表示一个"鱼骨"， $\mathit{AB}$ 平行于车辆前行方向， $\mathit{BE}\perp \mathit{AB}$ ， $\angle \mathit{CBE}=\alpha$ ，过 $B$ 作 $\mathit{AD}$ 的垂线，垂足为 $A\text{'}(A$ 点的视觉错觉点），若 $\sin \alpha =0.05$ ， $\mathit{AB}=300\mathit{mm}$ ，则 $\mathit{AA}\text{'}=$ 　　 $\mathit{mm}$ ．

如图，某梯子长10米，斜靠在竖直的墙面上，当梯子与水平地面所成角为 $\alpha$ 时，梯子顶端靠在墙面上的点 $A$ 处，底端落在水平地面的点 $B$ 处，现将梯子底端向墙面靠近，使梯子与地面所成角为 $\beta$ ，已知 $\sin \alpha =\cos \beta =\frac{3}{5}$ ，则梯子顶端上升了 $($ 　　 $)$

A．

1米

B．

1.5米

C．

2米

D．

2.5米

为进一步加强疫情防控工作，避免在测温过程中出现人员聚集现象，某学校决定安装，该设备通过探测人体红外辐射能量对进入测温区域的人员进行快速测温，无需人员停留和接触，安装说明书的部分内容如表．

名称	红外线体温检测仪
安装示意图
技术参数	探测最大角： $\angle \mathit{OBC}＝73.14°$
	探测最小角： $\angle \mathit{OAC}＝30.97°$
安装要求	本设备需安装在垂直于水平地面AC的支架CP上

根据以上内容，解决问题：

学校要求测温区域的宽度AB为4m，请你帮助学校确定该设备的安装高度OC．

（结果精确到0.1m，参考数据： $\mathit{sin}73.14°\approx 0.957，\mathit{cos}73.14°\approx 0.290$，t $\mathit{an}73.14°\approx 3.300$， $\mathit{sin}30.97°\approx 0.515$， $\mathit{cos}30.97°\approx 0.857$， $\text{t}\mathit{an}30.97°\approx 0.600$）

如图，著名旅游景区 $B$位于大山深处，原来到此旅游需要绕行 $C$地，沿折线 $A\to C\to B$方可到达．当地政府为了增强景区的吸引力，发展壮大旅游经济，修建了一条从 $A$地到景区 $B$的笔直公路．请结合 $\angle A=45°$， $\angle B=30°$， $\mathit{BC}=100$千米， $\sqrt{2}\approx 1.4$， $\sqrt{3}\approx 1.7$等数据信息，解答下列问题：

（1）公路修建后，从 $A$地到景区 $B$旅游可以少走多少千米？

（2）为迎接旅游旺季的到来，修建公路时，施工队使用了新的施工技术，实际工作时每天的工效比原计划增加 $25\%$，结果提前50天完成了施工任务．求施工队原计划每天修建多少千米？

人字梯为现代家庭常用的工具（如图）．若 $\mathit{AB}$， $\mathit{AC}$的长都为 $2m$，当 $\alpha =50°$时，人字梯顶端离地面的高度 $\mathit{AD}$是　 　 $m$．（结果精确到 $0.1m$，参考依据： $\sin 50°\approx 0.77$， $\cos 50°\approx 0.64$， $\tan 50°\approx 1.19)$

今年疫情期间，针对各种入口处人工测量体温存在的感染风险高、效率低等问题，清华大学牵头研制一款“测温机器人”，如图1，机器人工作时，行人抬手在测温头处测量手腕温度，体温合格则机器人抬起臂杆行人可通行，不合格时机器人不抬臂杆并报警，从而有效阻隔病原体．

（1）为了设计“测温机器人”的高度，科研团队采集了大量数据．下表是抽样采集某一地区居民的身高数据：

测量对象	男性 $(18~60$岁）				女性 $(18~55$岁）
抽样人数（人 $)$	2000	5000	20000	2000		5000	20000
平均身高（厘米）	173	175	176	164		165	164

根据你所学的知识，若要更准确的表示这一地区男、女的平均身高，男性应采用　176　厘米，女性应采用　　厘米；

（2）如图2，一般的，人抬手的高度与身高之比为黄金比时给人的感觉最舒适，由此利用（1）中的数据得出测温头点 $P$距地面105厘米．指示牌挂在两臂杆 $\mathit{AB}$， $\mathit{AC}$的连接点 $A$处， $A$点距地面110厘米．臂杆落下时两端点 $B$， $C$在同一水平线上， $\mathit{BC}=100$厘米，点 $C$在点 $P$的正下方5厘米处．若两臂杆长度相等，求两臂杆的夹角．

（参考数据表）

计算器按键顺序	计算结果（近似值）	计算器按键顺序	计算结果（近似值）
	0.1		78.7
	0.2		84.3
	1.7		5.7
	3.5		11.3

人字折叠梯完全打开后如图1所示， $B$， $C$是折叠梯的两个着地点， $D$是折叠梯最高级踏板的固定点．图2是它的示意图， $\mathit{AB}=\mathit{AC}$， $\mathit{BD}=140\mathit{cm}$， $\angle \mathit{BAC}=40°$，求点 $D$离地面的高度 $\mathit{DE}$．（结果精确到 $0.1\mathit{cm}$；参考数据 $\sin 70°\approx 0.94$， $\cos 70°\approx 0.34$， $\sin 20°\approx 0.34$， $\cos 20°\approx 0.94)$

如图1为搭建在地面上的遮阳棚，图2、图3是遮阳棚支架的示意图．遮阳棚支架由相同的菱形和相同的等腰三角形构成，滑块 $E$， $H$可分别沿等长的立柱 $\mathit{AB}$， $\mathit{DC}$上下移动， $\mathit{AF}=\mathit{EF}=\mathit{FG}=1m$．

（1）若移动滑块使 $\mathit{AE}=\mathit{EF}$，求 $\angle \mathit{AFE}$的度数和棚宽 $\mathit{BC}$的长．

（2）当 $\angle \mathit{AFE}$由 $60°$变为 $74°$时，问棚宽 $\mathit{BC}$是增加还是减少？增加或减少了多少？

（结果精确到 $0.1m$，参考数据： $\sqrt{3}\approx 1.73$， $\sin 37°\approx 0.60$， $\cos 37°\approx 0.80$， $\tan 37°\approx 0.75)$

图1是由七根连杆链接而成的机械装置，图2是其示意图．已知 $O$， $P$两点固定，连杆 $\mathit{PA}=\mathit{PC}=140\mathit{cm}$， $\mathit{AB}=\mathit{BC}=\mathit{CQ}=\mathit{QA}=60\mathit{cm}$， $\mathit{OQ}=50\mathit{cm}$， $O$， $P$两点间距与 $\mathit{OQ}$长度相等．当 $\mathit{OQ}$绕点 $O$转动时，点 $A$， $B$， $C$的位置随之改变，点 $B$恰好在线段 $\mathit{MN}$上来回运动．当点 $B$运动至点 $M$或 $N$时，点 $A$， $C$重合，点 $P$， $Q$， $A$， $B$在同一直线上（如图 $3)$．

（1）点 $P$到 $\mathit{MN}$的距离为　　 $\mathit{cm}$．

（2）当点 $P$， $O$， $A$在同一直线上时，点 $Q$到 $\mathit{MN}$的距离为　　 $\mathit{cm}$．

图1是一种三角车位锁，其主体部分是由两条长度相等的钢条组成．当位于顶端的小挂锁打开时，钢条可放入底盒中（底盒固定在地面下），此时汽车可以进入车位；当车位锁上锁后，钢条按图1的方式立在地面上，以阻止底盘高度低于车位锁高度的汽车进入车位．图2是其示意图，经测量，钢条 $\mathit{AB}=\mathit{AC}=50\mathit{cm}$， $\angle \mathit{ABC}=47°$．

（1）求车位锁的底盒长 $\mathit{BC}$．

（2）若一辆汽车的底盘高度为 $30\mathit{cm}$，当车位锁上锁时，问这辆汽车能否进入该车位？

（参考数据： $\sin 47°\approx 0.73$， $\cos 47°\approx 0.68$， $\tan 47°\approx 1.07)$

如图是小明画的卡通图形，每个正六边形的边长都相等，相邻两正六边形的边重合，点 $A$， $B$， $C$均为正六边形的顶点， $\mathit{AB}$与地面 $\mathit{BC}$所成的锐角为 $\beta$．则 $\tan \beta$的值是　　．