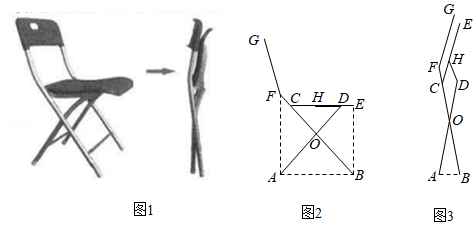
图1是某折叠式靠背椅实物图,图2是椅子打开时的侧面示意图,椅面 与地面平行,支撑杆 , 可绕连接点 转动,且 ,椅面底部有一根可以绕点 转动的连杆 ,点 是 的中点, , 均与地面垂直,测得 , , .
(1)椅面 的长度为 .
(2)如图3,椅子折叠时,连杆 绕着支点 带动支撑杆 , 转动合拢,椅面和连杆夹角 的度数达到最小值 时, , 两点间的距离为 (结果精确到 .
(参考数据: , ,
某种落地灯如图1所示, 为立杆,其高为 ; 为支杆,它可绕点 旋转,其中 长为 ; 为悬杆,滑动悬杆可调节 的长度.支杆 与悬杆 之间的夹角 为 .
(1)如图2,当支杆 与地面垂直,且 的长为 时,求灯泡悬挂点 距离地面的高度;
(2)在图2所示的状态下,将支杆 绕点 顺时针旋转 ,同时调节 的长(如图 ,此时测得灯泡悬挂点 到地面的距离为 ,求 的长.(结果精确到 ,参考数据: , , , , ,

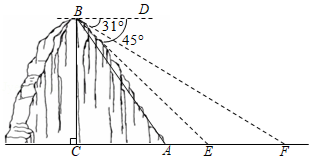
某镇为创建特色小镇,助力乡村振兴,决定在辖区的一条河上修建一座步行观光桥.如图,该河旁有一座小山,山高 ,坡面 的坡度 (注:坡度 是指坡面的铅直高度与水平宽度的比),点 、 与河岸 、 在同一水平线上,从山顶 处测得河岸 和对岸 的俯角分别为 , .
(1)求山脚 到河岸 的距离;
(2)若在此处建桥,试求河宽 的长度.(结果精确到
(参考数据: , ,
如图,点 为正六边形 对角线 上一点, , ,则 的值是

| A. |
20 |
B. |
30 |
| C. |
40 |
D. |
随点 位置而变化 |
试题篮
()