图1是第七届国际数学教育大会 会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形 .若 , ,则 的值为
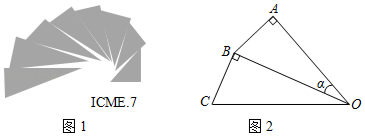
| A. |
|
B. |
|
C. |
|
D. |
|
如图,为了测量某建筑物 的高度,小颖采用了如下的方法:先从与建筑物底端 在同一水平线上的 点出发,沿斜坡 行走130米至坡顶 处,再从 处沿水平方向继续前行若干米后至点 处,在 点测得该建筑物顶端 的仰角为 ,建筑物底端 的俯角为 ,点 、 、 、 、 在同一平面内,斜坡 的坡度 .根据小颖的测量数据,计算出建筑物 的高度约为(参考数据:

| A. |
136.6米 |
B. |
86.7米 |
C. |
186.7米 |
D. |
86.6米 |
某限高曲臂道路闸口如图所示, 垂直地面 于点 , 与水平线 的夹角为 , ,若 米, 米,车辆的高度为 (单位:米),不考虑闸口与车辆的宽度:
①当 时, 小于3.3米的车辆均可以通过该闸口;
②当 时, 等于2.9米的车辆不可以通过该闸口;
③当 时, 等于3.1米的车辆不可以通过该闸口.
则上述说法正确的个数为

| A. |
0个 |
B. |
1个 |
C. |
2个 |
D. |
3个 |
如图,某梯子长10米,斜靠在竖直的墙面上,当梯子与水平地面所成角为 时,梯子顶端靠在墙面上的点 处,底端落在水平地面的点 处,现将梯子底端向墙面靠近,使梯子与地面所成角为 ,已知 ,则梯子顶端上升了

| A. |
1米 |
B. |
1.5米 |
C. |
2米 |
D. |
2.5米 |
如图,在距某居民楼 楼底 点左侧水平距离 的 点处有一个山坡,山坡 的坡度(或坡比) ,山坡坡底 点到坡顶 点的距离 ,在坡顶 点处测得居民楼楼顶 点的仰角为 ,居民楼 与山坡 的剖面在同一平面内,则居民楼 的高度约为(参考数据: , ,

A. B. C. D.
如图,两根竹竿 和 斜靠在墙 上,量得 , ,则竹竿 与 的长度之比为

A. B. C. D.
一座楼梯的示意图如图所示, 是铅垂线, 是水平线, 与 的夹角为 .现要在楼梯上铺一条地毯,已知 米,楼梯宽度1米,则地毯的面积至少需要

A. 米 B. 米 C. 米 D. 米
把直尺、三角尺和圆形螺母按如图所示放置于桌面上, ,若量出 ,则圆形螺母的外直径是
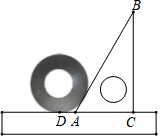
A. B. C. D.
如图,电线杆 的高度为 ,两根拉线 与 相互垂直, ,则拉线 的长度为 、 、 在同一条直线上)

A. B. C. D.
如图,已知在Rt△ABC中, ,点D沿BC自B向C运动(点D与点B、C不重合),作 于E, 于F,则BE+CF的值( )

A.不变B.增大
C.减小D.先变大再变小
如图,厂房屋顶人字形(等腰三角形)钢架的跨度BC=10米,∠B=36°,则中柱AD(D为底边中点)的长是( )

A.5sin36°米B.5cos36°米C.5tan36°米D.10tan36°米
构建几何图形解决代数问题是"数形结合"思想的重要性,在计算 时,如图.在 中, , ,延长 使 ,连接 ,得 ,所以 .类比这种方法,计算 的值为

| A. |
|
B. |
|
C. |
|
D. |
|
如图,某停车场入口的栏杆 ,从水平位置绕点 旋转到 的位置,已知 的长为4米.若栏杆的旋转角 ,则栏杆 端升高的高度为

| A. |
米 |
B. |
米 |
C. |
米 |
D. |
米 |
公元三世纪,我国汉代数学家赵爽在注解《周髀算经》时给出的"赵爽弦图"如图所示,它是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.如果大正方形的面积是125,小正方形面积是25,则

| A. |
|
B. |
|
C. |
|
D. |
|
试题篮
()