为了解某地七年级学生身高情况,随机抽取部分学生,测得他们的身高(单位:,并绘制了如下两幅不完整的统计图,请结合图中提供的信息,解答下列问题.
(1)填空:样本容量为 , ;
(2)把频数分布直方图补充完整;
(3)若从该地随机抽取1名学生,估计这名学生身高低于的概率.

为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
分数段 |
频数 |
频率 |
2 |
0.05 |
|
0.2 |
||
12 |
0.3 |
|
14 |
||
4 |
0.1 |
(1)表中 ,
;
(2)请在图中补全频数直方图;
(3)甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(4)选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.

某校数学活动小组对经过某路段的小型汽车每车乘坐人数(含驾驶员)进行了随机调查,根据每车乘坐人数分为5类,每车乘坐1人、2人、3人、4人、5人分别记为、
、
、
、
,由调查所得数据绘制了如图所示的不完整的统计图表.
类别 |
频率 |
0.35 |
|
0.20 |
|
0.05 |
(1)求本次调查的小型汽车数量及,
的值;
(2)补全频数分布直方图;
(3)若某时段通过该路段的小型汽车数量为5000辆,请你估计其中每车只乘坐1人的小型汽车数量.

文明交流互鉴是推动人类文明进步和世界和平发展的重要动力.2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注.某市一研究机构为了了解岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了尚不完整的频数分布表、频数分布直方图和扇形统计图,如下所示:
组别 |
年龄段 |
频数(人数) |
第1组 |
5 |
|
第2组 |
||
第3组 |
35 |
|
第4组 |
20 |
|
第5组 |
15 |

(1)请直接写出 ,
,第3组人数在扇形统计图中所对应的圆心角是 度.
(2)请补全上面的频数分布直方图;
(3)假设该市现有岁的市民300万人,问
岁年龄段的关注本次大会的人数约有多少?
争创全国文明城市,从我做起,某学校在七年级开设了文明礼仪校本课程,为了解学生的学习情况,学校随机抽取30名学生进行测试,成绩如下(单位:分)
78 83 86 86 90 94 97 92 89 86 84 81 81 84 86 88 92 89 86 83 81 81 85 86 89 93 93 89 85 93
整理上面的数据得到频数分布表和频数分布直方图:
成绩(分 |
频数 |
5 |
|
11 |
|
2 |
回答下列问题:
(1)以上30个数据中,中位数是 ;频数分布表中 ;
;
(2)补全频数分布直方图;
(3)若成绩不低于86分为优秀,估计该校七年级300名学生中,达到优秀等级的人数.

某校为了解学生课外阅读情况,就学生每周阅读时间随机调查了部分学生,调查结果按性别整理如下:
女生阅读时间人数统计表
阅读时间 |
人数 |
占女生人数百分比 |
4 |
||
5 |
||
6 |
||
2 |
根据图表解答下列问题:
(1)在女生阅读时间人数统计表中, ,
;
(2)此次抽样调查中,共抽取了 名学生,学生阅读时间的中位数在 时间段;
(3)从阅读时间在小时的5名学生中随机抽取2名学生参加市级阅读活动,恰好抽到男女生各一名的概率是多少?

某体育老师统计了七年级甲、乙两个班女生的身高,并绘制了以下不完整的统计图.

请根据图中信息,解决下列问题:
(1)两个班共有女生多少人?
(2)将频数分布直方图补充完整;
(3)求扇形统计图中部分所对应的扇形圆心角度数;
(4)身高在的5人中,甲班有3人,乙班有2人,现从中随机抽取两人补充到学校国旗队.请用列表法或画树状图法,求这两人来自同一班级的概率.
某校举行了自贡市创建全国文明城市知识竞赛活动,初一年级全体同学参加了知识竞赛.
收集教据:现随机抽取了初一年级30名同学的“创文知识竞赛”成绩,分数如下(单位:分)
90 85 68 92 81 84 95 93 87 89 78 99 89 85 97
88 81 95 86 98 95 93 89 86 84 87 79 85 89 82
整理分析数据:
成绩 |
频数(人数) |
1 |
|
2 |
|
17 |
|
|
(1)请将图表中空缺的部分补充完整;
(2)学校决定表彰“创文知识竞赛”成绩在90分及其以上的同学.根据上面统计结果估计该校初一年级360人中,约有多少人将获得表彰;
(3)“创文知识竞赛”中,受到表彰的小红同学得到了印有龚扇、剪纸、彩灯、恐龙图案的四枚纪念章,她从中选取两枚送给弟弟,则小红送给弟弟的两枚纪念章中,恰好有恐龙图案的概率是 .
胜利中学为丰富同学们的校园生活,举行“校园电视台主待人“选拔赛,现将36名参赛选手的成绩(单位:分)统计并绘制成频数分布直方图和扇形统计图,部分信息如下:

请根据统计图的信息,解答下列问题:
(1)补全频数分布直方图,并求扇形统计图中扇形对应的圆心角度数;
(2)成绩在区域的选手,男生比女生多一人,从中随机抽取两人临时担任该校艺术节的主持人,求恰好选中一名男生和一名女生的概率.
如图表示的是某班部分同学衣服上口袋的数目.


①从图中给出的信息得到学生衣服上口袋数目的中位数为 ,众数为 .
②根据如图信息,在给出的图表中绘制频数条形统计图,由此估计该班学生衣服上口袋数目为的概率.
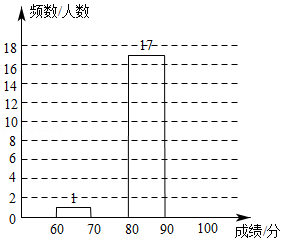
在“创全国文明城市”活动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中、
两小区分别有500名居民,社区从中各随机抽取50名居民进行相关知识测试,并将成绩进行整理得到部分信息:
[信息一]小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值);
[信息二]图中,从左往右第四组的成绩如下
75 |
75 |
79 |
79 |
79 |
79 |
80 |
80 |
81 |
82 |
82 |
83 |
83 |
84 |
84 |
84 |
[信息三]、
两小区各50名居民成绩的平均数、中位数、众数、优秀率
分及以上为优秀)、方差等数据如下(部分空缺)
小区 |
平均数 |
中位数 |
众数 |
优秀率 |
方差 |
75.1 |
79 |
277 |
|||
75.1 |
77 |
76 |
211 |
根据以上信息,回答下列问题:
(1)求小区50名居民成绩的中位数.
(2)请估计小区500名居民中能超过平均数的有多少人?
(3)请尽量从多个角度比较、分析,
两小区居民掌握垃圾分类知识的情况.
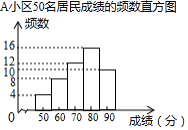
今年5月15日,亚洲文明对话大会在北京开幕.为了增进学生对亚洲文化的了解,某学校开展了相关知识的宣传教育活动.为了解这次宣传活动的效果,学校从全校1200名学生中随机抽取100名学生进行知识测试(测试满分100分,得分均为整数),并根据这100人的测试成绩,制作了如下统计图表.
100名学生知识测试成绩的频数表
成绩 |
频数(人 |
10 |
|
15 |
|
40 |
|
15 |
由图表中给出的信息回答下列问题:
(1) ,并补全频数直方图;
(2)小明在这次测试中成绩为85分,你认为85分一定是这100名学生知识测试成绩的中位数吗?请简要说明理由;
(3)如果80分以上(包括80分)为优秀,请估计全校1200名学生中成绩优秀的人数.

在推进嘉兴市城乡生活垃圾分类的行动中,某社区为了了解居民掌握垃圾分类知识的情况进行调查.其中、
两小区分别有500名居民参加了测试,社区从中各随机抽取50名居民成绩进行整理得到部分信息:
[信息一]小区50名居民成绩的频数直方图如图(每一组含前一个边界值,不含后一个边界值)
[信息二]上图中,从左往右第四组的成绩如下:
75 |
75 |
79 |
79 |
79 |
79 |
80 |
80 |
81 |
82 |
82 |
83 |
83 |
84 |
84 |
84 |
[信息三]、
两小区各50名居民成绩的平均数、中位数、众数、优秀率
分及以上为优秀)、方差等数据如下(部分空缺)
小区 |
平均数 |
中位数 |
众数 |
优秀率 |
方差 |
75.1 |
75 |
79 |
277 |
||
75.1 |
77 |
76 |
211 |
根据以上信息,回答下列问题:
(1)求小区50名居民成绩的中位数.
(2)请估计小区500名居民成绩能超过平均数的人数.
(3)请尽量从多个角度,选择合适的统计量分析,
两小区参加测试的居民掌握垃圾分类知识的情况.

为落实视力保护工作,某校组织七年级学生开展了视力保健活动.活动前随机测查了30名学生的视力,活动后再次测查这部分学生的视力.两次相关数据记录如下:
活动前被测查学生视力数据:
4.0 4.1 4.1 4.2 4.2 4.3 4.3 4.4 4.4 4.4 4.5 4.5 4.6 4.6 4.6
4.7 4.7 4.7 4.7 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 5.0 5.0 5.1
活动后被测查学生视力数据:
4.0 4.2 4.3 4.4 4.4 4.5 4.5 4.6 4.6 4.6 4.7 4.7 4.7 4.7 4.8
4.8 4.8 4.8 4.8 4.8 4.8 4.9 4.9 4.9 4.9 4.9 5.0 5.0 5.1 5.1
活动后被测查学生视力频数分布表
分组 |
频数 |
1 |
|
2 |
|
7 |
|
12 |
|
4 |
根据以上信息回答下列问题:
(1)填空: ,
,活动前被测查学生视力样本数据的中位数是 ,活动后被测查学生视力样本数据的众数是 ;
(2)若视力在4.8及以上为达标,估计七年级600名学生活动后视力达标的人数有多少?
(3)分析活动前后相关数据,从一个方面评价学校开展视力保健活动的效果.

中华人民共和国第二届青年运动会(简称二青会)将于2019年8月在山西举行.太原市作为主赛区,将承担多项赛事,现正从某高校的甲、乙两班分别招募10人作为颁奖礼仪志愿者,同学们踊跃报名,甲、乙两班各报了20人,现已对他们进行了基本素质测评,满分10分.各班按测评成绩从高分到低分的顺序各录用10人,对这次基本素质测评中甲、乙两班学生的成绩绘制了如图所示的统计图.请解答下列问题:
(1)甲班的小华和乙班的小丽基本素质测评成绩都为7分,请你分别判断小华,小丽能否被录用(只写判断结果,不必写理由).
(2)请你对甲、乙两班各被录用的10名志愿者的成绩作出评价(从“众数”,“中位数”,或“平均数”中的一个方面评价即可).
(3)甲、乙两班被录用的每一位志愿者都将通过抽取卡片的方式决定去以下四个场馆中的两个场馆进行颁奖礼仪服务,四个场馆分别为:太原学院足球场,太原市沙滩排球场,山西省射击射箭训练基地,太原水上运动中心,这四个场馆分别用字母,
,
,
表示.现把分别印有
,
,
,
的四张卡片(除字母外,其余都相同)背面朝上,洗匀放好.志愿者小玲从中随机抽取一张(不放回),再从中随机抽取一张,请你用列表或画树状图的方法求小玲抽到的两张卡片恰好是“
”和“
”的概率.
试题篮
()