初中数学统计表解答题

每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：

八年级抽取的学生的竞赛成绩：

4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．

七、八年级抽取的学生的竞赛成绩统计表

年级	七年级	八年级
平均数	7.4	7.4
中位数	a	b
众数	7	c
合格率	85%	90%

根据以上信息，解答下列问题：

（1）填空：a＝　　，b＝　　，c＝　　；

（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；

（3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异．

为弘扬传统文化，某校开展了“传承经典文化，阅读经典名著”活动．为了解七、八年级学生（七、八年级各有600名学生）的阅读效果，该校举行了经典文化知识竞赛．现从两个年级各随机抽取20名学生的竞赛成绩（百分制）进行分析，过程如下：

收集数据：

七年级：79，85，73，80，75，76，87，70，75，94，75，79，81，71，75，80，86，59，83，77．

八年级：92，74，87，82，72，81，94，83，77，83，80，81，71，81，72，77，82，80，70，41．

整理数据：

	$40⩽x⩽49$	$50⩽x⩽59$	$60⩽x⩽69$	$70⩽x⩽79$	$80⩽x⩽89$	$90⩽x⩽100$
七年级	0	1	0	$a$	7	1
八年级	1	0	0	7	$b$	2

分析数据：

	平均数	众数	中位数
七年级	78	75	$c$
八年级	78	$d$	80.5

应用数据：

（1）由上表填空： $a=$　　， $b=$　　， $c=$　　， $d=$　　．

（2）估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人？

（3）你认为哪个年级的学生对经典文化知识掌握的总体水平较好，请说明理由．

某校开展对学生“劳动习惯”情况的调查，为了解全校500名学生“主动做家务事”的情况，随机抽查了该校部分学生一周“主动做家务事”的次数，制成了如下的统计表和统计图．

次数	0	1	2	3	4
人数	3	6	13		12

（1）根据以上信息，求在被抽查学生中，一周“主动做家务事”3次的人数；

（2）若在被抽查学生中随机抽取1名，则抽到的学生一周“主动做家务事”不多于2次的概率是多少？

（3）根据样本数据，估计全校学生一周“主动做家务事”3次的人数．

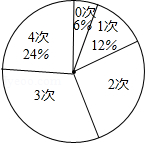
学校开展“书香校园”活动以来，受到同学们的广泛关注，学校为了解全校学生课外阅读的情况，随机调查了部分学生在一周内借阅图书的次数，并制成如图不完整的统计表．

学生借阅图书的次数统计表

借阅图书的次数	0次	1次	2次	3次	4次及以上
人数	7	13	$a$	10	3

请你根据统计图表中的信息，解答下列问题：

（1） $a=$　　， $b=$　　．

（2）该调查统计数据的中位数是　　，众数是　　．

（3）请计算扇形统计图中“3次”所对应扇形的圆心角的度数；

（4）若该校共有2000名学生，根据调查结果，估计该校学生在一周内借阅图书“4次及以上”的人数．

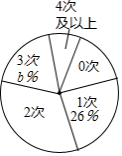
为了庆祝中国共产党建党100周年，某校开展了学党史知识竞赛．参加知识竞赛的学生分为甲乙两组，每组学生均为20名，赛后根据竞赛成绩得到尚不完整的统计图表（如图），已知竞赛成绩满分为100分，统计表中 $a$， $b$满足 $b=2a$．请根据所给信息，解答下列问题：

甲组20名学生竞赛成绩统计表

成绩（分 $)$	70	80	90	100
人数	3	$a$	$b$	5

（1）求统计表中 $a$， $b$的值；

（2）小明按以下方法计算甲组20名学生竞赛成绩的平均分是： $(70+80+90+100)÷4=85$（分 $)$．根据所学统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果；

（3）如果依据平均成绩确定竞赛结果，那么竞赛成绩较好的是哪个组？请说明理由．

为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）

节目类型	新闻	体育	动画	娱乐	戏曲
人数	36	90	$a$	$b$	27

根据表、图提供的信息，解决以下问题：

（1）计算出表中 $a$、 $b$的值；

（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；

（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？

为积极响应“弘扬传统文化”的号召，某学校倡导全校1200名学生进行经典诗词诵背活动，并在活动之后举办经典诗词大赛，为了解本次系列活动的持续效果，学校团委在活动启动之初，随机抽取部分学生调查“一周诗词诵背数量”，根据调查结果绘制成的统计图（部分）如图所示．

大赛结束后一个月，再次抽查这部分学生“一周诗词诵背数量”，绘制成统计表

一周诗词诵背数量	3首	4首	5首	6首	7首	8首
人数	10	10	15	40	25	20

请根据调查的信息分析：

（1）活动启动之初学生“一周诗词诵背数量”的中位数为　　；

（2）估计大赛后一个月该校学生一周诗词诵背6首（含6首）以上的人数；

（3）选择适当的统计量，从两个不同的角度分析两次调查的相关数据，评价该校经典诗词诵背系列活动的效果．

达州市图书馆今年4月23日开放以来，受到市民的广泛关注 $.5$月底，八年级（1）班学生小颖对全班同学这一个多月来去新图书馆的次数做了调查统计，并制成了如图不完整的统计图表．

八年级（1）班学生去新图书馆的次数统计表

去图书馆的次数	0次	1次	2次	3次	4次及以上
人数	8	12	$a$	10	4

请你根据统计图表中的信息，解答下列问题：

（1）填空： $a=$　　， $b=$　　；

（2）求扇形统计图中“0次”的扇形所占圆心角的度数；

（3）从全班去过该图书馆的同学中随机抽取1人，谈谈对新图书馆的印象和感受．求恰好抽中去过“4次及以上”的同学的概率．

在读书月活动中，某校号召全体师生积极捐书，为了解所捐书籍的种类，图书管理员对部分书籍进行了抽样调查，根据调查数据绘制了如下不完整的统计图表．请你根据统计图表所提供的信息回答下面问题：

某校师生捐书种类情况统计表

种类	频数	百分比
A．科普类	12	n
B．文学类	14	35%
C．艺术类	m	20%
D．其它类	6	15%

（1）统计表中的m＝　　，n＝　　；

（2）补全条形统计图；

（3）本次活动师生共捐书2000本，请估计有多少本科普类图书？

新冠疫情期间，某校开展线上教学，有“录播”和“直播”两种教学方式供学生选择其中一种．为分析该校学生线上学习情况，在接受这两种教学方式的学生中各随机抽取40人调查学习参与度，数据整理结果如表（数据分组包含左端值不包含右端值）．

参与度 人数 方式	$0.2~0.4$	$0.4~0.6$	$0.6~0.8$	$0.8~1$
录播	4	16	12	8
直播	2	10	16	12

（1）你认为哪种教学方式学生的参与度更高？简要说明理由．

（2）从教学方式为“直播”的学生中任意抽取一位学生，估计该学生的参与度在0.8及以上的概率是多少？

（3）该校共有800名学生，选择“录播”和“直播”的人数之比为 $1:3$，估计参与度在0.4以下的共有多少人？

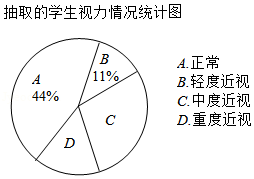
在创建"浙江省健康促进学校"的过程中，某数学兴趣小组针对视力情况随机抽取本校部分学生进行调查，并按照国家分类标准统计人数，绘制成两幅不完整的统计图表，请根据图表信息解答下列问题：

抽取的学生视力情况统计表

类别	检查结果	人数
$A$	正常	88
$B$	轻度近视	▲
$C$	中度近视	59
$D$	重度近视	▲

（1）求所抽取的学生总人数；

（2）该校共有学生约1800人，请估算该校学生中，近视程度为中度和重度的总人数；

（3）请结合上述统计数据，为该校做好近视防控，促进学生健康发展提出一条合理的建议．

为了庆祝中国共产党建党100周年，某校开展了学党史知识竞赛．参加知识竞赛的学生分为甲乙两组，每组学生均为20名，赛后根据竞赛成绩得到尚不完整的统计图表（如图），已知竞赛成绩满分为100分，统计表中 $a$， $b$满足 $b=2a$．请根据所给信息，解答下列问题：

甲组20名学生竞赛成绩统计表

成绩（分 $)$	70	80	90	100
人数	3	$a$	$b$	5

（1）求统计表中 $a$， $b$的值；

（2）小明按以下方法计算甲组20名学生竞赛成绩的平均分是： $(70+80+90+100)÷4=85$（分 $)$．根据所学统计知识判断小明的计算是否正确，若不正确，请写出正确的算式并计算出结果；

（3）如果依据平均成绩确定竞赛结果，那么竞赛成绩较好的是哪个组？请说明理由．

2020年我国进行了第七次全国人口普查，小星要了解我省城镇及乡村人口变化情况，根据贵州省历次人口普查结果，绘制了如下的统计图表．请利用统计图表提供的信息回答下列问题：

贵州省历次人口普查城镇人口统计表

年份	1953	1961	1982	1990	2000	2010	2020
城镇人口（万人）	110	204	540	635	845	1175	2050
城镇化率	$7\%$	$12\%$	$19\%$	$20\%$	$24\%$	$a$	$53\%$

（1）这七次人口普查乡村人口数的中位数是 　　万人；

（2）城镇化率是一个国家或地区城镇人口占其总人口的百分率，是衡量城镇化水平的一个指标．根据统计图表提供的信息，我省2010年的城镇化率 $a$ 是 　　（结果精确到 $1\%)$ ；假设未来几年我省城乡总人口数与2020年相同，城镇化率要达到 $60\%$ ，则需从乡村迁入城镇的人口数量是 　　万人（结果保留整数）；

（3）根据贵州省历次人口普查统计图表，用一句话描述我省城镇化的趋势．

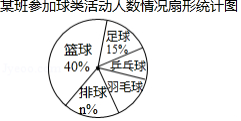
为了推进球类运动的发展，某校组织校内球类运动会，分篮球、足球、排球、羽毛球、乒乓球五项，要求每位学生必须参加一项并且只能参加一项，某班有一名学生根据自己了解的班内情况绘制了如图所示的不完整统计表和扇形统计图．

某班参加球类活动人数统计表

项目	篮球	足球	排球	羽毛球	乒乓球
人数	$m$	6	8	6	4

请根据图表中提供的信息，解答下列问题：

（1）图表中 $m=$　　， $n=$　　；

（2）若该校学生共有1000人，则该校参加羽毛球活动的人数约为　　人；

（3）该班参加乒乓球活动的4位同学中，有3位男同学（分别用 $A$， $B$， $C$表示）和1位女同学（用 $D$表示），现准备从中选出两名同学参加双打比赛，用树状图或列表法求出恰好选出一男一女的概率．

为了深化教育改革，某校计划开设四个课外兴趣活动小组：音乐、体育、美术、舞蹈，学校要求每名学生都自主选择其中一个兴趣活动小组，为此学校采取随机抽样的方式进行了问卷调查，对调查结果进行统计并绘制了如下统计表．

选择课程	音乐	体育	美术	舞蹈
所占百分比	$a$	$30\%$	$b$	$c$

根据以上统计图表中的信息，解答下列问题：

（1）本次调查的总人数为　　人；其中 $a=$　　 $\%$； $b=$　　 $\%$； $c=$　　 $\%$；

（2）请把条形图补充完整；

（3）若该校共有学生1000名，请估计该校选择“美术”的学生有多少人．