初中数学对称式和轮换对称式解答题

如图，在平面直角坐标系中，已知△ABC的三个顶点的坐标分别为A（﹣4，3）、B（﹣3，1）、C（﹣1，3）．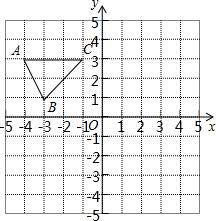

（1）请按下列要求画图：
①将△ABC先向右平移4个单位长度、再向上平移2个单位长度，得到△A₁B₁C₁，画出△A₁B₁C₁；
②△A₂B₂C₂与△ABC关于原点O成中心对称，画出△A₂B₂C₂．
（2）在（1）中所得的△A₁B₁C₁和△A₂B₂C₂关于点M成中心对称，请直接写出对称中心M点的坐标．

请分别画出下图中各图的所有对称轴．
（1）正方形       （2）正三角形         （3）相交的两个圆

如图，方格纸中的每个小正方形边长都是1个长度单位，Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A的坐标为（1，1），点B的坐标为（4，1）．
（1）先将Rt△ABC向左平移5个单位长度，再向下平移1个单位长度得到Rt△A₁B₁C₁，试在图中画出Rt△A₁B₁C₁，并写出点A₁的坐标；
（2）再将Rt△A₁B₁C₁绕点A₁顺时针旋转90°后得到Rt△A₂B₂C₂，试在图中画出Rt△A₂B₂C₂，并计算Rt△A₁B₁C₁在上述旋转过程中点C₁所经过的路径长．

如图1，在△ABC中，AB=AC，射线BP从BA所在位置开始绕点B顺时针旋转，旋转角为α（0°＜α＜180°）
（1）当∠BAC=60°时，将BP旋转到图2位置，点D在射线BP上．若∠CDP=120°，则∠ACD     ∠ABD（填“＞”、“=”、“＜”），线段BD、CD与AD之间的数量关系是     ；
（2）当∠BAC=120°时，将BP旋转到图3位置，点D在射线BP上，若∠CDP=60°，求证：BD﹣CD=AD；
（3）将图3中的BP继续旋转，当30°＜α＜180°时，点D是直线BP上一点（点P不在线段BD上），若∠CDP=120°，请直接写出线段BD、CD与AD之间的数量关系（不必证明）．

如图，△AOB是等边三角形，C为AB上一点，△OAC沿顺时针方向旋转后到达△OBD的位置．
（1）旋转中心是哪一点？
（2）旋转了多少度？
（3）如果点E为OA的中点，那么经过上述旋转后，点E旋转到了什么位置？

画出△ABC关于x轴对称的图形△A₁B₁C₁，并写出△A₁B₁C₁的顶点坐标.

如图，一块边长为8米的正方形土地，在上面修了三条道路，宽都是1米，空白的部分种上各种花草．
（1）请利用平移的知识求出种花草的面积．
（2）若空白的部分种植花草共花费了4620元，则每平方米种植花草的费用是多少元？

如图，在边长为1的小正方形组成的10×10网格中（我们把组成网格的小正方形的顶点称为格点），四边形ABCD在直线l的左侧，其四个顶点A、B、C、D分别在网格的格点上．

（1）请你在所给的网格中画出四边形A′B′C′D′，使四边形A′B′C′D′和四边形ABCD关于直线l对称，其中点A′、B′、C′、D′分别是点A、B、C、D的对称点；
（2）在（1）的条件下，结合你所画的图形，直接写出线段A′B′的长度．

画图并填空：
（1）画出图中△ABC的高AD（标注出点D的位置）；
（2）画出把△ABC沿射线AD方向平移3cm后得到的△A₁B₁C₁；
（3）根据“图形平移”的性质，得BB₁=            cm，AC与A₁C₁的位置关系是：            

在△ABC中，∠C=90°，AC=6，BC=8，DE垂直平分AB，求BE的长．

在数学兴趣小组活动中，小明进行数学探究活动，将边长为2的正方形ABCD与边长为2的正方形AEFG按图1位置放置，AD与AE在同一直线上，AB与AG在同一直线上．
（1）小明发现DG⊥BE，请你帮他说明理由．
（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．
（3）如图3，小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△GHE与△BHD面积之和的最大值，并简要说明理由．

某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．

（1）求证：AM=AN；
（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．

如图，△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连结EC．

（1）求∠ECD的度数；
（2）若CE=12，求BC长．

问题：如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，试判断BE、EF、FD之间的数量关系．
【发现证明】
小聪把△ABE绕点A逆时针旋转90°至△ADG，从而发现EF=BE+FD，请你利用图（1）证明上述结论．
【类比引申】
如图（2），四边形ABCD中，∠BAD≠90°，AB=AD，∠B+∠D=180°，点E、F分别在边BC、CD上，则当∠EAF与∠BAD满足∠BAD=2∠EAF关系时，仍有EF=BE+FD．
【探究应用】
如图（3），在某公园的同一水平面上，四条通道围成四边形ABCD．已知AB=AD=80米，∠B=60°，∠ADC=120°，∠BAD=150°，道路BC、CD上分别有景点E、F，且AE⊥AD，DF=40（﹣1）米，现要在E、F之间修一条笔直道路，求这条道路EF的长（结果取整数，参考数据：=1．41，=1．73）

如图，将三角形ABC绕点O旋转得到三角形A^/B^/C^/，且∠AOB=30⁰，∠AOB^/=20⁰，则
（1）点B的对应点是________________;
（2）线段OB的对应线段是____________;
（3）∠AOB的对应角是________________;
（4）三角形ABC旋转的角度是__________;