在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:
(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点 的坐标为(1,3),那么不等式
的坐标为(1,3),那么不等式 的解集是 .
的解集是 .
(本题10分)同学们都知道: 表示
表示 与
与 之差的绝对值,实际上也可理解为
之差的绝对值,实际上也可理解为 与
与 两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:
两数在数轴上所对应的两点之间的距离.请你借助数轴进行以下探索:

(1) 数轴上表示 与
与 两点之间的距离是________,
两点之间的距离是________,
(2) 数轴上表示 与
与 的两点之间的距离可以表示为__ ________.
的两点之间的距离可以表示为__ ________.
(3) 如果 ,则
,则 = .
= .
(4) 同理 表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得
表示数轴上有理数x所对应的点到-3和1所对应的点的距离之和,请你找出所有符合条件的整数x,使得 =4,这样的整数是 .
=4,这样的整数是 .
(5) 由以上探索猜想对于任何有理数 ,
, 是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
是否有最小值?如果有,直接写出最小值;如果没有,说明理由.
试验与探究:我们知道分数 写为小数即
写为小数即 ,反之,无限循环小数
,反之,无限循环小数 写成分数即
写成分数即 .一般地,任何一个无限循环小数都可以写成分数形式.现在就以
.一般地,任何一个无限循环小数都可以写成分数形式.现在就以 为例进行讨论:设
为例进行讨论:设  ,由
,由 …,可知,
…,可知, 7.777… —0.777… =7,即
7.777… —0.777… =7,即  ,解方程得
,解方程得 于是得,
于是得, .
.
请仿照上述例题完成下列各题:
(1)请你能把无限循环小数 写成分数,即
写成分数,即 = .
= .
(2)你能化无限循环小数  为分数吗?请仿照上述例子求解之.
为分数吗?请仿照上述例子求解之.
如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
在“家电下乡”活动期间,凡购买指定家用电器的农村居民均可得到每购买1元商品政府给予0.13元的财政补贴.村民小李购买了一台A型洗衣机,小王购买了一台B型洗衣机,两人一共得到财政补贴351元,又知B型洗衣机售价比A型洗衣机售价多500元.试求:
(1)A型洗衣机和B型洗衣机的售价各是多少元?
(2)小李和小王购买洗衣机除财政补贴外实际各付款多少元?
2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
据电力部门统计,每天8︰00至21︰00是用点高峰期,简称“峰时”,21︰00至次日8︰00是用电低谷期,简称“谷时”。为了缓解供电需求紧张的矛盾,我市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见下表:
| 时间 |
换表前 |
换表后 |
|
| 峰时(8︰00—21︰00) |
谷时(21︰00—8︰00) |
||
| 电价 |
每度0.52元 |
每度0.55元 |
每度0.30元 |
小明家对换表后最初使用的95度电进行测算,经测算比换表前使用95度电节约了5.9元,问小明家使用“峰时” 电和“谷时” 电分别是多少度?
(本题12分)如图,若点 在数轴上对应的数为
在数轴上对应的数为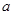 ,点
,点 在数轴上对应的数为
在数轴上对应的数为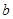 ,且
,且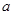 ,
,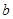 满足
满足 .点
.点 与点
与点 之间的距离表示为
之间的距离表示为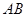 (以下类同).
(以下类同).
(1)求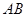 的长;
的长;
(2)点 在数轴上对应的数为
在数轴上对应的数为 ,且
,且 是方程
是方程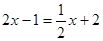 的解,在数轴上是否存在点
的解,在数轴上是否存在点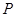 ,使得
,使得 ?若存在,求出点
?若存在,求出点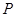 对应的数;若不存在,说明理由;
对应的数;若不存在,说明理由;
(3)在(1)、(2)的条件下,点 ,
, ,
,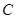 开始在数轴上运动,若点
开始在数轴上运动,若点 以每秒
以每秒 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点 和点
和点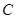 分别以每秒
分别以每秒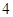 个单位长度和
个单位长度和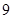 个单位长度的速度向右运动,经过
个单位长度的速度向右运动,经过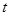 秒后,请问:
秒后,请问: 的值是否随着时间
的值是否随着时间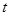 的变化而改变?若变化,请说明理由;若不变,请求其常数值.
的变化而改变?若变化,请说明理由;若不变,请求其常数值.
某服装厂生产一种西装和领带,西装每套定价200元,领带每条定价40元.厂方在开展促销活动期间,向客户提供两种优惠方案:
①买一套西装送一条领带;
②西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带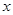 条(
条(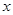 >20).
>20).
(1)若该客户按方案①购买,需付款________元(用含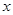 的代数式表示);若该客户按方案②购买,需付款________元(用含
的代数式表示);若该客户按方案②购买,需付款________元(用含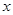 的代数式表示).
的代数式表示).
(2)若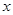 =30,通过计算说明此时按哪种方案购买较为合算?
=30,通过计算说明此时按哪种方案购买较为合算?
列方程解应用题:某商场以每台1980元的价格购进一批彩电,进货时按当时的市场行情,制定的销售价为每台2640元.销售一段时间后,由于市场竞争激烈,商场决定降价销售.如果销售每台仍能获利20%,那么应该按原销售价的几折出售?
阅读下列材料:
为落实开展社会大课堂活动,七年级(3)班李老师准备周六组织本班学生参观北京科技馆,要求学生周六早9:00准时在科技馆门前集合,然后几种买票参观.
小强家离北京科技馆4公里,周六他准备乘出租车去,为了解北京出租车的计价方式,小强周五晚上在网上查到了现行北京市出租车价格标准:
| 收费项目 |
收费标准 |
| 3公里以内收费 |
13元 |
| 基本单价 |
2.3元/公里 |
| 低速行驶和等候费 |
根据乘客要求停车等候或由于道路条件限制,时速低于12公里时,每5分钟早晚高峰期间加收2公里租价(不含空驶费)其他时间段加收1公里租价(不含空驶费) |
| 预约叫车服务费 |
提前4小时以上预约每次6元,4小时以内预约每次5元 |
| 空驶费 |
单程旅客行驶超过15公里部分,基本单价加收50%的费用,往返载客(即起点和终点在2公里(含)范围以内)不加收空驶费 |
| 夜间收费 |
23:00(含)至次日5:00(不含)运营时,基本单价加收20%的费用 |
| 合乘收费 |
合乘里程部分,按非合乘情况下应付金额的60%付费 |
| 燃油附加费 |
1元/运次 |
| 备注:1、早高峰7:00(含)﹣﹣9:00(不含);晚高峰17:00(含)﹣﹣19:00(不含). 2、出租车计价段里程精确到500米,时间精确到2.5分钟;出租汽车收费结算以元为单位,元以下四舍五入. 3、过路、过桥费由乘客负担. 4、按日结算的包车及出北京行政区域的客运业务收费实行市场调节价. |
在仔细阅读标准后,小强准备周六早上8点10分乘车,路上留出10分钟出租车时速低于12公里的堵车时间,这样在9点之前一定能顺利到达科技馆.时间设计好后,经过计算小强向妈妈要30元打车钱,妈妈问他30元钱够吗?小强说:“我按上表计算了,30元钱还有几块钱的剩余呢.”
下面是小强的分析与计算过程,请补充完整:
(1)小强在计算所需出租车费用时,用到上表中的信息包括 .
(2)路上堵车10分钟,小强计算这10分钟出租车的低速行驶费用是多少?
(3)小强说:“我按上表计算了,30元钱还有几块钱的剩余呢.”请你计算小强的打车费用和剩余钱数.
如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米,
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出正方形F、E和C的边长;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN和PQ).请根据这个等量关系,求出x的值;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问还要多少天完成?
(本题10分)用正方形硬纸板做三棱柱盒子,每个盒子由 个矩形侧面和
个矩形侧面和 个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)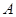 方法:剪
方法:剪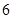 个侧面;
个侧面;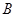 方法:剪
方法:剪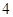 个侧面和
个侧面和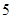 个底面.
个底面.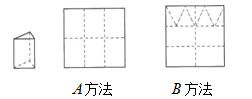
现有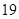 张硬纸板,裁剪时
张硬纸板,裁剪时 张用
张用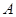 方法,其余用
方法,其余用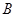 方法.
方法.
(1)用 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
如图:在数轴上A点表示数 ,B点示数
,B点示数 ,C点表示数c,b是最小的正整数,
,C点表示数c,b是最小的正整数,
且a、b满足|a+2|+ (c-7)2=0.
(1)a= ,b= ,c= ;
(2)若将数轴折叠,使得A点与C点重合,则点B与数 表示的点重合;
(3)点A、B、C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.
则AB= ,AC= ,BC= .(用含t的代数式表示)
(4)请问:3BC-2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
某地的一种绿色蔬菜,在市场上若直接销售,每吨利润为1000元,经粗加工后销售,每吨利润4000元,经精加工后销售,每吨利润7000元。当地一家公司现有这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨,如果对蔬菜进行精加工,每天可加工6吨,但每天两种方式不能同时进行.受季节等条件的限制,必须用15天时间将这批蔬菜全部销售或加工完毕.为此,公司研制了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能地对蔬菜进行精加工,没来得及加工的蔬菜,在市场上直接出售;
方案三:将一部分蔬菜进行精加工,其余蔬菜进行粗加工,并刚好15天完成.
如果你是公司经理,你会选择哪一种方案,说说理由.
试题篮
()