商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出场价分别为甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,该选择哪种进货方案?
下图的数阵是由一些奇数排成的.
(1)图框中的四个数有什么关系?(设框中第一行第一个数为 )
)
(2)若这样框出的四个数的和是200,求这四个数;
(3)是否存在这样的四个数,它们的和为420,为什么?
某商店在一次买卖中,同时卖出两件上衣,每件都以135元出售,按成本计算,其中一件盈利25%,另一件亏本25%.
(1)在这次买卖中,是赔是赚,还是不赔不赚?
(2)若将题中的135改成任意正数a,赔或赚的情况如何?
(本题12分)如图,若点 在数轴上对应的数为
在数轴上对应的数为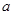 ,点
,点 在数轴上对应的数为
在数轴上对应的数为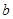 ,且
,且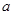 ,
,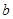 满足
满足 .点
.点 与点
与点 之间的距离表示为
之间的距离表示为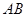 (以下类同).
(以下类同).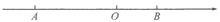
(1)求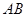 的长;
的长;
(2)点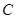 在数轴上对应的数为
在数轴上对应的数为 ,且
,且 是方程
是方程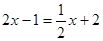 的解,在数轴上是否存在点
的解,在数轴上是否存在点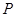 ,使得
,使得 ?若存在,求出点
?若存在,求出点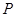 对应的数;若不存在,说明理由;
对应的数;若不存在,说明理由;
(3)在(1)、(2)的条件下,点 ,
, ,
,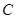 开始在数轴上运动,若点
开始在数轴上运动,若点 以每秒
以每秒 个单位长度的速度向左运动,同时,点
个单位长度的速度向左运动,同时,点 和点
和点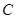 分别以每秒
分别以每秒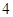 个单位长度和
个单位长度和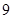 个单位长度的速度向右运动,经过
个单位长度的速度向右运动,经过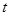 秒后,请问:
秒后,请问: 的值是否随着时间
的值是否随着时间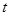 的变化而改变?若变化,请说明理由;若不变,请求其常数值.
的变化而改变?若变化,请说明理由;若不变,请求其常数值.
(本题12分)阅读下列材料并解决有关问题:
我们知道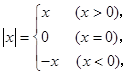 现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式
现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式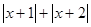 时,可令
时,可令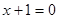 和
和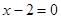 ,分别求得
,分别求得 和
和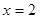 (称
(称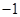 ,
,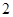 分别为
分别为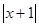 与
与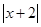 的零点值).在有理数范围内,零点值
的零点值).在有理数范围内,零点值 和
和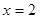 可将全体有理
可将全体有理数分成不重复且不遗漏的如下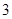 种情况:(1)
种情况:(1)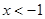 ;(2)
;(2) ;(3)
;(3) .从而化简代数式
.从而化简代数式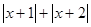 可分以下
可分以下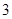 种情况:
种情况:
(1)当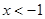 时,原式
时,原式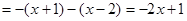 ;
;
(2)当 时,原式
时,原式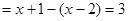 ;
;
(3)当 时,原式
时,原式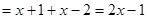 .
.
综上讨论,原式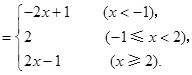
通过以上阅读,请你解决以下问题:
(1)分别求出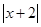 和
和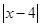 的零点值;
的零点值;
(2)化简代数式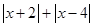 ;
;
(3)解方程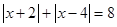 .
.
(本题10分)用正方形硬纸板做三棱柱盒子,每个盒子由 个矩形侧面和
个矩形侧面和 个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)
个正三角形底面组成,硬纸板以如图两种方法裁剪(裁剪后边角料不再利用)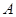 方法:剪
方法:剪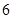 个侧面;
个侧面;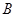 方法:剪
方法:剪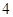 个侧面和
个侧面和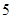 个底面.
个底面.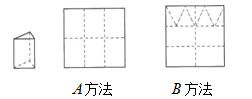
现有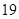 张硬纸板,裁剪时
张硬纸板,裁剪时 张用
张用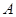 方法,其余用
方法,其余用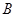 方法.
方法.
(1)用 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
试题篮
()