某体育用品商场采购员要到厂家批发购进篮球和排球共100只,付款总额不得超过11815元,已知两种球厂家的批发价和商场的零售价如下表,试解答下列问题:
| 品名 |
厂家批发价(元/只) |
市场零售价(元/只) |
| 篮球 |
130 |
160 |
| 排球 |
100 |
120 |
⑴该采购员最多可购进篮球多少只?
⑵若该商场把100只球全部以零售价售出,为使商场的利润不低于2590元,则采购员采购的方案有几种?
某公司拟为贫困山区建一所希望小学,甲、乙两个工程队提交了投标方案,若独立完成该项目,则甲工程队所用时间是乙工程队的1.5倍;若甲、乙两队合作完成该项目,则共需72天.
(1)甲、乙两队单独完成建校工程各需多少天?
(2)若由甲工程队单独施工,平均每天的费用为0.8万元,为了缩短工期,该公司选择了乙工程队,但要求其施工的总费用不能超过甲工程队,求乙工程队平均每天的施工费用最多为多少万元?
(本题10分)若不等式组 的解集是
的解集是 ,
,
(1)求代数式 的值;
的值;
(2)若 ,
, ,
, 为某三角形的三边长,试求
为某三角形的三边长,试求 的值.
的值.
2013年4月20日,四川雅安发生7.0级地震,给雅安人民的生命财产带来巨大损失.某市民政部门将租用甲、乙两种货车共16辆,把粮食266吨、副食品169吨全部运到灾区.已知一辆甲种货车同时可装粮食18吨、副食品10吨;一辆乙种货车同时可装粮食16吨、副食11吨.
(1)若将这批货物一次性运到灾区,有哪几种租车方案?
(2)若甲种货车每辆需付燃油费1500元;乙种货车每辆需付燃油费1200元,应选(1)中的哪种方案,才能使所付的费用最少?最少费用是多少元?
小明参加学校组织的知识竞赛,共有 道题.答对一题记
道题.答对一题记 分,答错(或不答)一题记
分,答错(或不答)一题记 分,小明参加本次竞赛要超过
分,小明参加本次竞赛要超过 分,他至少要答对多少道题?
分,他至少要答对多少道题?
纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒.
(1)现有正方形纸板172张,长方形纸板330张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
 纸盒 纸盒纸板 |
竖式纸盒(个) |
横式纸盒(个) |
| x |
|
|
| 正方形纸板(张) |
|
2(100-x) |
| 长方形纸板(张) |
4x |
|
②按两种纸盒的数量分,有哪几种生产方案?
(2)若有正方形纸板112张,长方形纸板 张,做成上述两种纸盒,纸板恰好用完.已知100<
张,做成上述两种纸盒,纸板恰好用完.已知100< <110,则
<110,则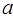 的值是 .
的值是 .
对x,y定义一种新运算T,规定:T(x,y)=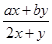 (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= =b.
=b.
(1)已知T(1,-1)=-2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
雅安地震后,政府为安置灾民,从某厂调拨了用于搭建板房的板材5600m2和铝材2210m,计划用这些材料在某安置点搭建甲、乙两种规格的板房共100间,若搭建一间甲型板房或一间乙型板房所需板材和铝材的数量如下表所示:
| 板房规格 |
板材数量(m2) |
铝材数量(m) |
| 甲型 |
40 |
30 |
| 乙型 |
60 |
20 |
请你根据以上信息,设计出甲、乙两种板房的搭建方案.
先阅读短文,然后回答短文后面所给出的问题:
对于三个数a、b、c的平均数,最小的数都可以给出符号来表示,我们规定 表示这三个数的平均数,
表示这三个数的平均数,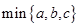 表示这三个数中的最小的数,
表示这三个数中的最小的数, 表示这三个数中最大的数.例如:
表示这三个数中最大的数.例如: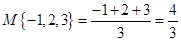 ,
,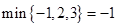 ,
,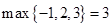 ;
; ,
, .
.
(1)请填空: ;若
;若 ,则
,则 ;
;
(2)若 ,求
,求 的取值范围;
的取值范围;
(3)若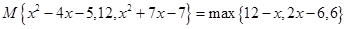 ,求
,求 的值.
的值.
郑州市花卉种植专业户王有才承包了30亩花圃,分别种植康乃馨和玫瑰花,有关成本、销售额见下表:
| 种植种类 |
成本(万元/亩) |
销售额(万元/亩) |
| 康乃馨 |
2.4 |
3 |
| 玫瑰花 |
2 |
2.5 |
(1)2012年,王有才种植康乃馨20亩、玫瑰花10亩,求王有才这一年共收益多少万元?(收益=销售额-成本)
(2)2013年,王有才继续用这30亩花圃全部种植康乃馨和玫瑰花,计划投入成本不超过70万元.若每亩种植的成本、销售额与2012年相同,要获得最大收益,他应种植康乃馨和玫瑰花各多少亩?
(3)已知康乃馨每亩需要化肥500kg,玫瑰花每亩需要化肥700kg,根据(2)中的种植亩数,为了节约运输成本,实际使用的运输车辆每次装载化肥的总量是原计划每次装载总量的2倍,结果运输全部化肥比原计划减少2次.求王有才原定的运输车辆每次可装载化肥多少千克?
对x,y定义一种新运算T,规定:T(x,y)= (其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=
(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)= =b.
=b.
(1)已知T(1,-1)=-2,T(4,2)=1.
①求a,b的值;
②若关于m的不等式组 恰好有3个整数解,求实数p的取值范围;
恰好有3个整数解,求实数p的取值范围;
(2)若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?
学校计划选购甲、乙两种图书作为“校园读书节”的奖品.已知甲图书的单价是乙图书单价的1.5倍;用600元单独购买甲种图书比单独购买乙种图书要少10本.
(1)甲、乙两种图书的单价分别为多少元?
(2)若学校计划购买这两种图书共40本,且投入的经费不超过1050元,要使购买的甲种图书数量不少于乙种图书的数量,则共有几种购买方案?
某公司生产的一种健身产品在市场上受到普遍欢迎,每年可在国内、国外市场上全部售完,该公司的年产量为6千件,若在国内市场销售,平均每件产品的利润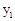 (元)与国内销售数量
(元)与国内销售数量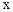 (千件)的关系为:
(千件)的关系为: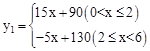 若在国外销售,平均每件产品的利润
若在国外销售,平均每件产品的利润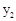 (元)与国外的销售数量t(千件)的关系为:
(元)与国外的销售数量t(千件)的关系为:
(1)用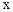 的代数式表示t为:t= ;当0<
的代数式表示t为:t= ;当0<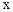 ≤4时,
≤4时,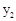 与
与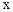 的函数关系式为:
的函数关系式为: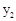 = ;当4≤
= ;当4≤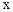 < 时,
< 时,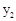 =100;
=100;
(2)求每年该公司销售这种健身产品的总利润W(千元)与国内的销售数量x(千件)的函数关系式,并指出x的取值范围;
(3)该公司每年国内、国外的销量各为多少时,可使公司每年的总利润最大?最大值为多少?
试题篮
()