初中数学应用类问题解答题

“五一”期间，为了满足广大人民的消费需求，某商店计划用160 000元购进一批家电，这批家电的进价和售价如下表：

(1)若全部资金用来购买彩电和洗衣机共100台，则商家可以购买彩电和洗衣机各多少台？
(2)若在现有资金160 000元允许的范围内，购买上表中三类家电共100台，其中彩电台数和冰箱台数相同，且购买洗衣机的台数不超过购买彩电的台数，请你算一算，共有几种进货方案？哪种进货方案能使商店销售完这批家电后获得的利润最大？并求出最大利润．（利润＝售价－进价）

．我市某镇的一种特产由于运输原因，长期只能在当地销售．当地政府对该特产的销售投资收益为：每投入x万元，可获得利润P＝－(x－60)²＋41（万元）．当地政府拟在“十二•五”规划中加快开发该特产的销售，其规划方案为：在规划前后对该项目每年最多可投入100万元的销售投资，在实施规划5年的前两年中，每年都从100万元中拨出50万元用于修建一条公路，两年修成，通车前该特产只能在当地销售；公路通车后的3年中，该特产既在本地销售，也在外地销售．在外地销售的投资收益为：每投入x万元，可获利润Q＝－(100－x)²＋(100－x)＋160（万元）．
（1）若不进行开发，求5年所获利润的最大值是多少？
（2）若按规划实施，求5年所获利润（扣除修路后）的最大值是多少？
（3）根据（1）、（2），该方案是否具有实施价值？

如图1，过△ABC的三个顶点分别作出与水平线垂直的三条直线，外侧两条直线之间的距离叫△ABC的“水平宽”(a)，中间的这条直线在△ABC内部线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法：，即三角形面积等于水平宽与铅垂高乘积的一半.

解答下列问题：
如图2，抛物线顶点坐标为点C(1,4),交x轴于点A(3,0)，交y轴于点B.
（1）求抛物线和直线AB的解析式；
（2）点P是抛物线(在第一象限内)上的一个动点，连结PA，PB，当P点运动到顶点C时，求△CAB的铅垂高CD及；
  （3）是否存在一点P，使S_△PAB=S_△CAB，若存在，求出P点的坐标；若不存在，请说明理由.

观察下面三行数
1，－2，4，－8，16，－32 ……  ①
0，－6，6，－18，30，－66 …… ②
2，－4，8，－16，32，－64 …… ③
第③行的数按什么规律排列？
第①、②行的数与第③行的数分别有什么关系？
取每行数的第8个数，计算它们的和。

小王购买了一套经济适用房，他准备将地面铺上地砖，地面结构如图所示。根据图中的数据（单位：m），解答下列问题：

①用含、的代数式表示地面总面积；
②当，时，若铺1m²地砖的平均费用为80元，那么铺地砖的总费用为多元？

佳佳和小超玩一个抽卡片游戏：有一叠卡片，每张上面都写着一个数字，二人轮流从中抽取，若抽到的卡片上的数字大于10，就加上这个数字，若抽到的卡片上的数字不大于10，就减去这个数字.第一轮抽卡完毕（每人抽4张），二人抽到的卡片如下图所示.若规定从0开始计算，结果小者为胜，那么第一轮抽卡谁获胜？

(10分）某人在银行的信用卡存入2万元，每次取出50元，若卡内余额为 y（元），取钱的次数为x.(利息忽略不计）
（1）、写出y与x之间的函数关系式，并求出自变量的取值范围？
（2）、取多少次钱以后，余额为原存款的四分之一？

．何老师在黑板上出了一道题：当x=2010，y=2009时，[2x(x²y-xy²)+xy(2xy-x²)]÷x²y的值.题目出完后，小玉同学说：“老师给的条件y=2009是多余的.”小丹同学说：“不给这个条件就不能求出结果，所以不是多余的.”你认为她们谁说的有道理？为什么？

(本题8分)如图，在梯形ABCD中，AB∥DC，AB＝14cm，CD＝6cm.点P从点A出发，以2cm/s的速度沿AB向终点B运动；点Q从点C出发，以1cm/s的速度沿CD向终点Ｄ运动(P、Q两点中，有一个点运动到终点时，所有运动即终止)，设P、Q同时出发并运动了t秒。
(1)当DQ=AP时，四边形APQD是平形四边形，求出此时t的值；
(2) 试问在这样的运动过程中，是否存在某一时刻，使梯形PBCQ的面积是梯形ABCD面积的一半?若存在，求出这样的t的值，若不存在，请说明理由。

 

在一块长16m，宽12m的矩形荒地上，要建造一个花园，要求花园面积是荒地面积的一半，下面分别是小华与小芳的设计方案.

方案是否符合条件有不同意见，你认为小芳的方案符合条件吗？若不符合，请用方程的方法说明理由.
你还有其他的设计方案吗？请在图9-3中画出你所设计的草图，将花园部分涂上阴影，并加以说明.

（本小题共5分）一家三口在假期期间去北方旅游，当地有甲、乙两家旅游社，其定价一样，但对家庭旅游都有优惠，甲旅行社表示大人不打折，小孩打六折；乙旅行社表示一家三口全都打八折，经核算，乙旅行社要便宜240元，问成人定价多少元？

夏天容易发生腹泻等肠道疾病，某市医药公司的甲、乙两仓库分别存有医治腹泻的药品80箱和70箱，现需要将库存的药品调往A地100箱和B地50箱。已知从甲、乙两仓库运送药品到两地的费用（元／箱）如下表所示：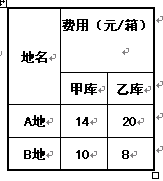

设从甲仓库运送到A地的药品为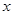箱，求总费用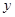（元）与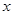（箱）之间的函数关系式，并写出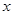的取值范围
求出最低费用，并说明总费用最低时的调配方案

用火柴摆出下列一组图形：

⑴．填写下表：

图形编号	⑴	⑵	⑶	⑷	⑸	⑹
图形中的火柴数

⑵．照这样的方式摆下去，写出摆第个图形火柴的根数；
⑶．如果某一图形共有97根火柴，你知道它是第几个图形吗？

按下面的要求填空，完成本题的解答．
青山村种的水稻2007年平均每公顷产8 000 kg，2009年平均每公顷产9 680 kg，
求该村水稻每公顷产量的年平均增长率.
解：设该村水稻每公顷产量的年平均增长率为.
（Ⅰ）用含的代数式表示：
① 2008年种的水稻平均每公顷的产量为                      kg；
② 2009年种的水稻平均每公顷的产量为                      kg；
（Ⅱ）根据题意，列出相应方程                             ；
（Ⅲ）解这个方程，得                             ；
（Ⅳ）检验：                                                           ；
（Ⅴ）答：该村水稻每公顷产量的年平均增长率为                         %.

已知某市居民生活用电基本价格为每度0.45元，若每月用电量超过a度，超过部分按基本电价的70%收费。
（1）某户5月份用电84度，共缴电费30.72元，求a的值。
（2）若该户六月份的电费平均每度为0.36元，求6月份共用多少度电？应交电费多少元？