某水果批发市场经销一种水果,如果每千克盈利10元,每天可售出500千克.经市场调查发现,在进货价不变的情况下,若每千克这种水果在原售价的基础上每涨价1元,日销售量将减少20千克.如果市场某天销售这种水果盈利了6 000元,同时顾客又得到了实惠,那么每千克这种水果涨了多少元?
设每千克这种水果涨价x元时(0<x≤25),市场每天销售这种水果所获利润为y元.若不考虑其它因素,单纯从经济角度看,每千克这种水果涨价多少元时,市场每天销售这种水果盈利最多?最多盈利多少元?
某蒜薹生产基地喜获丰收,收获蒜薹200吨.经市场调查,可采用批发、零售、冷库储藏后销售三种方式,并按这三种方式销售,计划平均每吨的售价及成本如下表:
若经过一段时间,蒜薹按计划全部售出获得的总利润为y(元),蒜薹零售x(吨),且零售量是批发量的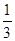 .
.求y与x之间的函数关系式;
由于受条件限制,经冷库储藏售出的蒜薹最多80吨,求该生产基地按计划全部售完蒜薹获得的最大利润.
温州市有一种可食用的野生菌,上市时,外商李经理按市场价格30元/千克收购了这种野生菌1000千克存放入冷库中,据预测,该野生菌的市场价格将以每天每千克上涨1元;但冷冻存放这批野生菌时每天需要支出各种费用合计310元,而且这类野生菌在冷库中最多保存160天,同时,平均每天有3千克的野生菌损坏不能出售。设
 天后每千克该野生菌的市场价格为
天后每千克该野生菌的市场价格为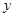 元,试写出
元,试写出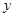 与
与 之间的函数关系式;
之间的函数关系式;若存放
 天后,将这批野生菌一次性出售,设这批野生菌的销售总额为
天后,将这批野生菌一次性出售,设这批野生菌的销售总额为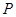 元,试写出
元,试写出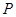 与
与 之间的函数关系式;
之间的函数关系式;李经理将这批野生菌存放多少天后出售可获得最大利润
 元?
元?
(利润=销售总额-收购成本-各种费用)
如图,已知抛物线 经过O(0,0),A(4,0),B(3,
经过O(0,0),A(4,0),B(3, )三点,连接AB,过点B作BC∥
)三点,连接AB,过点B作BC∥ 轴交该抛物线于点C.
轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为
 (秒) (0<
(秒) (0< ≤2),△PQA的面积记为S.
≤2),△PQA的面积记为S.
① 求S与 的函数关系式;
的函数关系式;
② 当 为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的
 值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
商场某种新商品每件进价是120元,在试销期间发现,当每件商品售价为130元时,每天可销售70件,当每件商品售价高于130元时,每涨价1元,日销售量就减少1件.据此规律,请回答:当每件商品售价定为170元时,每天可销售多少件商品?商场获得的日盈利是多少?
在上述条件不变、商品销售正常的情况下,每件商品的销售价定为多少元时,商场日盈利可达到1600元?(提示:盈利=售价-进价)
某超市经销一种销售成本为60元的商品,据超市调查发现,如果按每件70元销售,一周能销售500件,若销售单价每涨1元,每周销售减少10件,设销售价为每件x元(x≥70),一周的销售量为y件.写出y与x的函数关系式(标明x的取值范围).
设一周的销售利润为w,写出w与x的函数关系式,并确定当单价在什么范围内变化时,利润随着单价的增大而增大?
在超市对该商品投入不超过15000元的情况下,使得一周销售利润达到8000元,销售单价应定为多少?
农民张大伯为了致富奔小康,大力发展家庭养殖业,他准备用30米长的木栏围一个矩形的养圈,为了节约材料,同时要使矩形面积最大,他想利用自己家房屋一面长12米的墙.但张大伯不知矩形的长、宽各是多少时,面积最大.请你为张大伯设计一种方案,使矩形羊圈的面积最大?
在长方形中画出5条线,把它分成的块数与画线的方式有直接关系.按如图1的方式画线,可以把它分成10块.请你在图2中画出5条线,使得把这个长方形分成的块数最少(重合的线只看做一条),最少可分成 块;
请你在图2中画出5条线,使得把这个长方形分成的块数最多,最多可分成 块.
(画出图形不写画法和理由)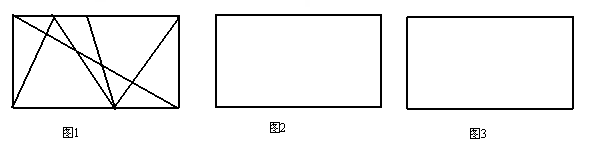
.某人2008年初投资120万元于股市,由于无暇操作,第一年的亏损率为20%,以后其亏损率有所变化,至2011年初其股票市值仅为77.76万元,求此人的股票在第二年、第三年平均每年的亏损率.
随着大陆惠及台胞政策措施的落实,台湾水果进入了大陆市场。一水果经销商购进了A,B两种台湾水果各10箱,分配给他的甲、乙两个零售店(分别简称甲店、乙店)销售。预计每箱水果的盈利情况如下表:
有两种配货方案(整箱配货):
方案一:甲、乙两店各配货10箱,其中A种水果两店各5箱,B种水果两店各5箱;
方案二:按照甲、乙两店盈利相同配货,其中A种水果甲店_________箱,乙店__________箱;B种水果甲店_________箱,乙店__________箱.如果按照方案一配货,请你计算出经销商能盈利多少元?
请你将方案二填写完整(只填写一种情况即可),并根据你填写的方案二与方案一作比较,哪种方案盈利较多?
在甲、乙两店各配货10箱,且保证乙店盈利不小于100元的条件下,请你设计出使水果经销商盈利最大的配货方案,并求出最大盈利为多少?
某公司近三年每年的资金投入总额与每年利润统计图如下,其中利润率=利润÷资金投入总额×100%.已知2010年的利润等于2009年、2010年两年的资金投放差额,并且三年的利润每年上升20万元.请在乙图中左侧横线上填上相关利润数据
请在丙图中大致画出三年的利润情况(标明度数、年份,不需标示百分比)
试确定哪一年的利润率最高?

试题篮
()