初中数学应用类问题试题

在开展“学雷锋社会实践”活动中，某校为了解全校1200名学生参加活动的情况，随机调查了50名学生每人参加活动的次数，并根据数据绘成条形统计图如下：

（1）求这50个样本数据的平均数、众数和中位数；
（2）根据样本数据，估算该校1200名学生共参加了多少次活动．

已知一个反比例函数的图象经过点．
（Ⅰ）求这个函数的解析式；
（Ⅱ）判断点是否在这个函数的图象上；
（Ⅲ）当时，求自变量的值．

（本小题满分12分）
如图是某月的日历：

(1)设由6个数形成的阴影方框中，最大的数为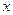，这6个数的和为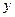，请你用含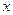的代数式表示；
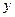(2)现想框出6个数的和为111，你能办得到吗？若能，请求出这六个数，若不能，请说明理由.

△ABC中，已知点D在边BC上，且BD=2DC，设=，=，则等于            .

如图，某轮船上午8时在A处，测得灯塔S在北偏东60°的方向上，向东行驶至中午12时，该轮船在B处，测得灯塔S在北偏西30°的方向上（自己完成图形），已知轮船行驶速度为每小时20千米，则∠ASB=＿＿＿＿＿＿，AB长为＿＿＿＿＿

按下面的程序计算，若开始输入的值x为正数，最后输出的结果为11，则满足条件的x的不同值分别为               .

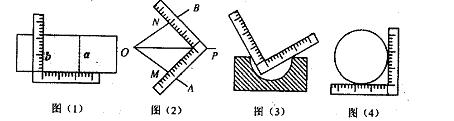
用一把带有刻度的直尺，① 可以画出两条平行的直线与b，如图⑴；② 可以画出∠AOB的平分线OP，如图⑵所示；③ 可以检验工件的凹面是否为半圆，如图⑶所示；④ 可以量出一个圆的半径，如图⑷所示．这四种说法正确的个数有 

A．1个

B．2个

C．3个

D．4个

《中华人民共和国道路交通管理条例》规定：小汽车在城市街道上行驶速度不得超过千米/小时，如图，一辆小汽车在一条城市街道上直道行驶，某一时刻刚好行驶到路对面车速检测仪正前方米点处，过了秒后，小汽车在点处测得与车速检测仪间距离为米，问：这辆小汽车超速了吗？

建设中的昆石高速公路，在某施工段上沿AC方向开山修路，为加快施工速度，要在山坡的另一边同时施工，如图所示，从AC上的一点B取∠ABD=150°，BD=380米，∠D=60°，那么开挖点E离D多远，正好使A、C、E成一直线．

观察下列顺序排列的等式：，…．试猜想第个等式（为正整数）：            ．

假期中，小明和同学们到某海岛上去探宝旅游，按照探宝图，他们从A点登陆后先往东走7千米，又往北走4千米，遇到障碍后又往西走了3千米，再折向北走了8千米处往东一拐，仅走了1千米就找到宝藏点B，问登陆点A到宝藏埋藏点B的距离是多少千米？

如图甲所示，在直角梯形ABCD中，AB∥DC，．动点P从点B出发，沿梯形的边由B→C→D→A运动．设点P运动的路程为x，△ABP的面积为y．把y看作x的函数，函数的图像如图乙所示，则△ABC的面积为(     )

A．10

B．16

C．18

D．32

数与数之间的关系真奇妙，例如：①；②；③．某教师分析如下：⑴以上这些等式都有一个共同特征：两个实数的差等于这两个实数的商；⑵如果等号左边的第一个实数用表示，第二个实数用表示，则可以得到一个关于的关系式．请你根据以上分析，再找出一组满足上述特征的两个实数，并写成等式形式：          ．

、阅读下列材料并填空。平面上有n个点（n≥2）且任意三个点不在同一条直线上，过这些点作直线，一共能作出多少条不同的直线？
①分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线……
②归纳：考察点的个数和可连成直线的条数发现：如下表

点的个数	可作出直线条数
2	1=
3	3=
4	6=
5	10=
……	……
n

③推理：平面上有n个点，两点确定一条直线。取第一个点A有n种取法，取第二个点B有（n－1）种取法，所以一共可连成n(n-1)条直线，但AB与BA是同一条直线，故应除以2；即
④结论：
试探究以下几个问题：平面上有n个点（n≥3），任意三个点不在同一条直线上，过任意三个点作三角形，一共能作出多少不同的三角形？
（1）分析：
当仅有3个点时，可作出      个三角形；
当仅有4个点时，可作出      个三角形；
当仅有5个点时，可作出      个三角形；
……
（2）归纳：考察点的个数n和可作出的三角形的个数，发现：（填下表）

点的个数	可连成三角形个数
3
4
5
……
n

 
(3)推理：                             
（4）结论：

尺规作图：（不写作法，保留作图痕迹）
        
已知：、，求作：∠ABC，使∠ABC=+。