初中数学二次函数在给定区间上的最值试题

某桥洞是呈抛物线形状，它的截面在平面直角坐标系中如图所示，现测得水面宽AB=16m，桥洞顶点O到水面距离为16m，当水面上升7m时，水面宽为           m．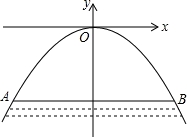

二次函数y=ax²+bx-c与一次函数y=ax+c在同一直角坐标系中图象大致是（    ）

关于二次函数y=（x-1）²+2，则下列说法正确的是（    ）

A．当x=1时，y有最大值为2

B．当x=1时，y有最小值为2

C．当x=-1时，y有最大值为2

D．当x=-1时，y有最小值为2

已知二次函数y=x²+2x-3．
（1）求此二次函数的图象与x轴的交点坐标；
（2）此二次函数的图象经怎样平移，使顶点变为A（3，0），请你描述平移的过程．

二次函数y=－x²+bx+c的部分图象如图所示，图象的对称轴为过点（－1，0）且平行于y轴的直线，图象与x轴交于点（1，0），则一元二次方程－x²+bx+c=0的根为    ．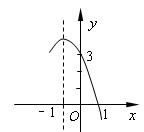

阅读材料，解答问题：
若两个二次函数图象的顶点，开口方向都相同，则称这两个二次函数为“同簇二次函数”．
（1）下列各组二次函数中，是“同簇二次函数”的是                （填序号）；
①y=x²+1与y=2x²；
②y=x²+2x+2与y=2（x-1）²+1；
③y=-x²-2x+3与y=-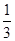（x+1）²+4
（2）已知关于x的二次函数y₁=2x²-4mx+2m²+1和y₂=ax²+bx+5，其中y₁的图象经过点A（1，1），若y₁+y₂与y₁为“同簇二次函数”，求函数y₂的表达式．

已知二次函数y=x²-3x+m（m为常数）的图象与x轴的一个交点为（1，0），则关于x的一元二次方程x²-3x+m=0的两实数根是             ．

如图，抛物线y=﹣x²+bx+c与x轴交于A（1，0），B（﹣4，0）两点，

（1）求该抛物线的解析式；
（2）设（1）中的抛物线交y轴于C点，在该抛物线的对称轴上是否存在点Q，使得?QAC的周长最小？若存在，求出Q点的坐标；若不存在，请说明理由；
（3）设此抛物线与直线y=﹣x在第二象限交于点D，平行于y轴的直线x=m（-1-＜m＜0）与抛物线交于点M，与直线y=﹣x交于点N，连接BM、CM、NC、NB，是否存在m的值，使四边形BNCM的面积S最大？若存在，请求出m的值，若不存在，请说明理由．

某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于65元，市场调查发现，若每箱以50元的价格出售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱．
（1）求平均每天销售量y（箱）与涨价x（元/箱）之间的函数关系式；
（2）求当每箱苹果的销售价为多少元，批发商平均每天的销售利润W（元）可以获得最大？

二次函数y=2（x﹣1）²+3的图象的顶点坐标是（  ）

A．（1，3）

B．（﹣1，3）

C．（1，﹣3）

D．（﹣1，﹣3）

将抛物线向左平移个单位长度，再向下平移个单位长度，得到的抛物线的函数表达式为（    ）

A．

B．

C．

D．

已知函数与x轴有且仅有一个交点，则的值是_________

二次函数y=－3x²+1的图象是将（   ）

A．抛物线y=－3x^2向左平移3个单位得到

B．抛物线y=－3x^2向左平移1个单位得到

C．抛物线y=—3x^2向上平移1个单位得到

D．抛物线y=3x^2向上平移1个单位得到

将抛物线的图象先向右平移2个单位，再向上平移3个单位后，得到的抛物线的解析式是（ ）

A．

B．

C．

D．

将抛物线向下平移2个单位长度，再向右平移2个单位长度后，得到抛物线的解析式为（     ）

A．	B．
C．	D．