抛物线y=﹣x2+(m﹣1)x+m与y轴交于点(0,3).
(1)求抛物线的解析式;
(2)求抛物线与坐标轴的交点坐标;
(3)①当x取什么值时,y>0?②当x取什么值时,y的值随x的增大而减小?
如图,在直角坐标平面内,直线y=-x+5与 轴和
轴和 轴分别交于A、B两点,二次函数y=
轴分别交于A、B两点,二次函数y= +bx+c的图象经过点A、B,且顶点为C.
+bx+c的图象经过点A、B,且顶点为C.
(1)求这个二次函数的解析式;
(2)求sin∠OCA的值;
(3)若P是这个二次函数图象上位于x轴下方的一点,且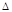 ABP的面积为10,求点P的坐标.
ABP的面积为10,求点P的坐标.
已知二次函数y=ax2+bx-3的图象经过点A(2,-3),B(-1,0).求二次函数的解析式
已知二次函数
(1)求它的顶点坐标和对称轴;
(2)画出这个函数的图象;
(3)根据图象回答:当 取哪些值时,
取哪些值时,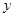 =0,
=0,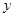 >0,
>0,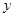 <0
<0
在一场2015亚洲杯赛B组第二轮比赛中,中国队凭借吴曦和孙可在下半场的两个进球,提前一轮小组出线。如图,足球场上守门员在 处开出一高球,球从离地面1米的
处开出一高球,球从离地面1米的 处飞出(
处飞出( 在
在 轴上),运动员孙可在距
轴上),运动员孙可在距 点6米的
点6米的 处发现球在自己头的正上方达到最高点
处发现球在自己头的正上方达到最高点 ,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
,距地面约4米高,球落地后又一次弹起.据实验测算,足球在草坪上弹起后的抛物线与原来的抛物线形状相同,最大高度减少到原来最大高度的一半.
(1)求足球开始飞出到第一次落地时,该抛物线的函数表达式.
(2)足球第一次落地点 距守门员多少米?(取
距守门员多少米?(取 )
)
(3)孙可要抢到足球第二个落地点 ,他应从第一次落地点
,他应从第一次落地点 再向前跑多少米?(取
再向前跑多少米?(取 )
)
如图,抛物线经过A(4,0)、B(1,0)、C(0,-2)三点.
(1)求出抛物线的解析式;
(2)在直线AC上方的抛物线上有一动点D,当△ACD的面积最大时,求出点D的坐标;
(3)P是抛物线上一动点,过P作PM⊥x轴,垂足为M,是否存在P点,使得以A,P,M为顶点的三角形与△OAC相似?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由.
已知抛物线 y=ax2+bx+3 (a≠0) 经过A(5,0), B(6,1)两点,且与y轴交于点C.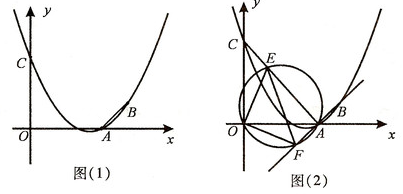
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A重合)经过A、E、O三点的圆交直线AB于点F,求出当△OEF的面积取得最小值时,点E的坐标.
如图,已知抛物线y=-ax2+2ax+3a(a≠0)与x轴交于A、B两点,与y轴交于点C.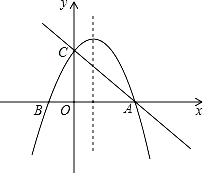
(1)请直接写出A、B两点的坐标.
(2)当a=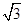 ,设直线AC与抛物线的对称轴交于点P,请求出△ABP的面积.
,设直线AC与抛物线的对称轴交于点P,请求出△ABP的面积.
如图,在平面直角坐标系xoy中,矩形ABCD的边AB在x轴上,且AB=3,BC=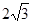 ,直线
,直线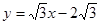 经过点C,交y轴于点G.
经过点C,交y轴于点G.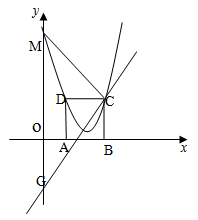
(1)求C,D坐标;
(2)已知抛物线顶点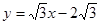 上,且经过C,D,若抛物线与y交于点M连接MC,设点Q是线段下方此抛物线上一点,当点Q运动到什么位置时,△MCQ的面积最大?求出此时点Q的坐标和面积的最大值.
上,且经过C,D,若抛物线与y交于点M连接MC,设点Q是线段下方此抛物线上一点,当点Q运动到什么位置时,△MCQ的面积最大?求出此时点Q的坐标和面积的最大值.
(3)将(2)中抛物线沿直线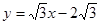 平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求 出此时抛物线的解析式;若不存在,请说明理由.
平移,平移后的抛物线交y轴于点F,顶点为点E(顶点在y轴右侧)。平移后是否存在这样的抛物线,使⊿EFG为等腰三角形?若存在,请求 出此时抛物线的解析式;若不存在,请说明理由.
已知二次函数y=x2+2x-3.
(1)求此二次函数的图象与x轴的交点坐标;
(2)此二次函数的图象经怎样平移,使顶点变为A(3,0),请你描述平移的过程.
如图,抛物线y=﹣x2+bx+c与x轴交于A(1,0),B(﹣4,0)两点,
(1)求该抛物线的解析式;
(2)设(1)中的抛物线交y轴于C点,在该抛物线的对称轴上是否存在点Q,使得?QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由;
(3)设此抛物线与直线y=﹣x在第二象限交于点D,平行于y轴的直线x=m(-1- <m<0)与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
<m<0)与抛物线交于点M,与直线y=﹣x交于点N,连接BM、CM、NC、NB,是否存在m的值,使四边形BNCM的面积S最大?若存在,请求出m的值,若不存在,请说明理由.
某水果批发商销售每箱进价为40元的苹果,物价部门规定每箱售价不得高于65元,市场调查发现,若每箱以50元的价格出售,平均每天销售90箱,价格每提高1元,平均每天少销售3箱.
(1)求平均每天销售量y(箱)与涨价x(元/箱)之间的函数关系式;
(2)求当每箱苹果的销售价为多少元,批发商平均每天的销售利润W(元)可以获得最大?
试题篮
()