初中数学二次函数在给定区间上的最值试题

某厂的年利润为50万元，年增长率为x, 第三年的利润为y万元，则y与x之间的函数关系式为____________.

周长为16cm的矩形的最大面积为____,此时矩形边长为____,实际上此时矩形是______.

已知一直角三角形两条直角边的和是6cm，则以这个直角三角形的斜边为边长的正方形的面积的最小值是______.

x人去旅游共需支出y元，若x,y之间满足关系式y="2x2" - 20x + 1050,则当人数为_____时总支出最少。

某商品进货单价为30元，按40元一个销售，能卖40个，若销售单价每涨一元，销售量就减少一个，则为了获得最大利润，此商品的最佳售价应为 _____元。

[应用题]如图,一单杠高2.2米,两立柱之间的距离为1.6米,将一绳子的两端拴于立柱与铁杠结合处,绳子自然下垂呈抛物线状.

（1）如图(1)一身高为0.7米的小孩站在离立柱0.4米处,其头部刚好触到绳子,求绳子最低点到地面的距离;
(2)如图(2),为供孩子们打秋千,把绳子剪断后,中间系一块长为0.4米的木板.除掉系木板用去的绳子后,两边的绳子长正好各为2米,木板与地面平行.求这时木板离地面的距离(参考数据:≈1.8, ≈1.9, ≈2.1).

已知：某租赁公司出租同一型号的设备40套，当每套月租金为270元时，恰好全部租出。在此基础上，每套月租金每增加10元，就少租出1套设备。而未租出的设备每月需支付各种费用每套20元。
设每套设备实际月租金为x元（x≥270元），月收益为y元（总收益＝设备租金收入－未租出设备费用）
问题1： 求y与x的二次函数关系式
问题2： 当x为何值时，月收益最大？最大值是多少？
问题3： 当月租金分别为300元/每套和350元/每套时，月收益各是多少？根据月收益的计算结果，此时公司应该选择出租多少套设备更合适，请简要说明理

某宾馆有50个房客供游客居住,当每个房间的定价为每天180元时,房间会全部住满,当每个房间的定价每增加10元时,就会有一个房间空闲,如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用。房价定为多少时，宾馆利润最大？

利达经销店为某工厂代销一种建筑材料(这里的代销指厂家先免费提供货源,待货物销售后再进行结算,末售出的由厂家负责处理).当每吨售价为260元时,月销售量为45吨.该经销店为提高利润,准备采取降价的方式进行促销.经市场调查发现: 当每吨售价每下降10元时, 月销售量就会增加7.5吨.综合考虑各种因素,每出售一吨建筑材料共需支付厂家和其
他费用100元.设每吨材料售价为x(元),该经销店的月销售量y(元).
(1)当每吨售价是240元时,计算此时的月销售量;
(2)求出y与x的关系式(不要求写出x的取值范围);
(3)该经销店要获得最大利润,售价应定为每吨多少元?
(4)小静说:“当月利润最大时,月销售额也最大”,你认为对吗?请说明理由.

如图在一块直角三角形铁皮废料的内部剪下一个长方形盒盖ABCD,其中ＡＢ和BC分别在两直角边上，设ＡＢ＝Ｘｃｍ，长方形盒盖的面积为ｙｃｍ２，要使长方形盒盖的面积最大，Ｘ应为（　　）

Ａ　　　Ｂ　６　　Ｃ１５　　Ｄ　

已知某商品销售利润y(元)与该商品销售单价x(元)之间满足y=-20x2+1400x-20000,则获利最多为（     ）
A   4500      B  5500        C  450    D  20000

一学生推铅球，铅球行进的高度y(m)与水平距离x(m)之间的关系式为y=-x2+x+,则铅球落地水平距离为（  ）m
A         B  3            C  10          D  12

有一拱桥的桥拱是抛物线形， 其表达式是Y=-0.25x²,
当桥下水面宽为12米时，水面到拱桥拱顶的距离为（       ）
A  3米        B 2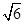米         C 4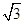米        D  9米

函数Y=X2+2X-3(-2≦X≦2)的最大值和最小值分别是（  ）  
A 4和-3   B -3和-4  C 5和-4   D -1和-4

周长为8米的铝合金条制成如图形状的窗框，使窗户的透光面积最大，则最大透光面积是____.