初中数学二次函数在给定区间上的最值选择题

若抛物线的顶点到轴的距离是3，则的值等于（  ）

A．8或14

B．14

C．-8

D．-8或-14

抛物线y=x²的图象向左平移2个单位，再向下平移1个单位，则所得抛物线的解析式为（    ）

A．y=x^2+4x+3

B．y=x^2+4x+5

C．y=x^2－4x+3

D．y=x^2－4x－5

下列函数不属于二次函数的是 （    ）

A．

B．

C．

D．

在平面直角坐标系中，如果抛物线y＝3x²不动，而把x轴、y轴分别向上、向右平移2个单位，那么在新坐标系下抛物线的解析式是 (       )

A．y＝3(x + 2)^2－2	B．y＝3(x－2)^2 + 2
C．y＝3(x－2)^2－2	D．y＝3(x + 2)^2 + 2

函数y=2x²+4x+1①；y=2x²－ 4x+1②的图象的位置关系是(　　 )

A．②在①的上方；

B．②在①的下方；

C．②在①的左方；

D．②在①的右方。

要从抛物线y=x²－3得到y=x²的图象，则抛物线y=x²－3必须(　　 ).

A．向上平移3个单位	B．向下平移3个单位
C．向左平移3个单位	D．向右平移3个单位

已知二次函数y=ax²+bx+c(a≠0)的图象如图所示，有下列5个结论：①abc＜0；②a－b+c＞0；③ 2a+b=0；④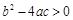 ⑤a+b+c＞m(am+b)+c，（m＞1的实数），其中正确的结论有（   ）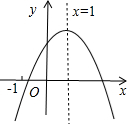

A．1个

B．2个

C．3个

D．4个

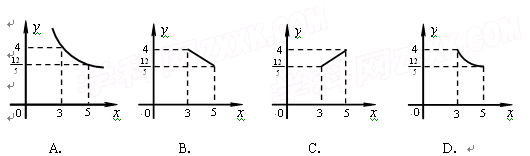
如图，在矩形ABCD中，AB＝4，BC＝3，点P在CD边上运动，联结AP，过点B作BE⊥AP，垂足为E，设AP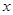＝，BE＝，则能反映与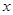之间函数关系的图象大致是（   ）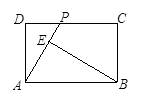

将抛物线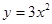先向左平移2个单位，再向下平移1个单位后得到新的抛物线，则
新抛物线的解析式是（    ）

A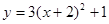．	B．
C．	D．

已知：，且=0，则二次函数的图象可能是下列图象中的（   ）．    

若抛物线C：y＝ax²＋bx＋c与抛物线y＝x²－2关于x轴对称，则抛物线C的解析式为

A．y＝x^2－2	B．y＝－x^2－2
C．y＝－x^2＋2	D．y＝x^2＋2

如果抛物线y＝－x²＋bx＋c经过A(0，－2)，B(－1，1)两点，那么此抛物线经过

A．第一、二、三、四象限	B．第一、二、三象限
C．第一、二、四象限	D．第二、三、四象限

抛物线y＝x²－4x＋5的顶点坐标是

A．(2，5)

B．(－2，5)

C．(2，1)

D．(－2，1)

已知点A(－1，0)在抛物线y＝ax²＋2上，则此抛物线的解析式为

A．y＝x^2＋2

B．y＝x^2－2

C．y＝－x^2＋2

D．y＝－2x^2＋2

已知：关于x的一元二次方程的一个根为，且二次函数的对称轴是直线，则抛物线的顶点坐标为                 (    )

A．(2，3)

B． (2，1)

C．

D．(3，2)