初中数学二次函数在给定区间上的最值选择题

下列各点在二次函数的图像上的是（ ）

A．（0，2）

B．（1，2）

C．（1，－2）

D．（，2）

将二次函数向左平移3个单位后得到的函数图像解析式为（）

A．

B．

C．

D．

已知点（﹣2，5），（4，5）是抛物线上的两点，则此抛物线的对称轴为( )

A．x=﹣2

B．x="2"

C．x="1"

D．无法确定

若是开口向下的抛物线，则m的值是（）

A．m＝3

B．m=-3

C．m=

D．m=

将抛物线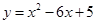向上平移2个单位长度，再向右平移1个单位长度后，得到的抛物线解析式是（）

A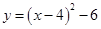．	B．
C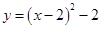．	D．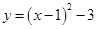

已知函数与轴交点是，则的值是（）

A．2013

B．2014

C．2015

D．2016

如图是二次函数y=ax²+bx+c（a≠0）图象的一部分，直线x=-1是对称轴，有下列判断：①b-2a=0；②4a-2b+c＜0；③a-b+c=-9a；④若（-3，y₁），（，y₂）是抛物线上两点，则y₁＞y₂，其中正确的个数是（）

A．1个

B．2个

C．3个

D．4个

在同一坐标系内，一次函数y=ax+b与二次函数y=ax²+8x+b的图象可能是（）

用配方法将二次函数y=x²-2x+1写成y=a（x-h）²+k的形式是（）

A．y=（x-2）²-1	B．y=（x-1）²-1
C．y=（x-2）²-3	D．y=（x-1）²-3

抛物线y=3x²，y=-3x²，y=x²+3共有的性质是（）

A．开口向上	B．对称轴是y轴
C．都有最高点	D．y随x值的增大而增大

关于抛物线y=(x-1)²-2，下列说法中错误的是

A．顶点坐标为(1，-2)

B．对称轴是直线x=1

C．当x＞1时，y随x的增大而减小

D．开口方向向上

抛物线y=x²+2x-1关于y轴对称的抛物线的解析式为 （）

A．y=x^2-2x-1	B．y=x^2-2x-3
C．y=-x^2+2x-3	D．y=-x^2-2x-1

二次函数y=ax²＋bx＋c的图象如图所示．现有下列4个判断：①ac＜0; ②a＋b=0;③4ac－b²=4a;④a＋b＋c＜0，其中正确的有（）

A．1个

B．2个

C．3个

D．4个

下列函数中，不是二次函数的是（）

A．y＝1－x^2

B．y＝2（x－1）^2＋4

C．y＝（x－1）（x＋4）

D．y＝（x－2）^2－x^2

函数y=与y=-kx²+k（k≠0）在同一直角坐标系中的图象可能是（）