初中数学二次函数在给定区间上的最值选择题

如图（1），点E为矩形ABCD边AD上一点，点P，Q同时从点B出发，点P沿BE→ED→DC运动到点C停止，点Q沿BC运动到点C停止，它们的运动速度都是1cm/s,设P，Q出发ts时，△BPQ的面积为ycm²，已知y与t的函数关系的图象如图（2）则下列正确的是（）

A．AE=6cm

B．sin∠EBC=

C．当0＜t≤10时，

D．当t=12时，△BPQ是等腰三角形

下列命题中，假命题的个数为（）
（1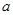）“是任意实数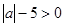，”是必然事件；
（2）抛物线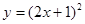的对称轴是直线；
（3）若某运动员投篮2次，投中1次，则该运动员投1次篮，投中的概率为；
（4）某件事情发生的概率是1，则它一定发生；
（5）某彩票的中奖率为10%，则买100张彩票一定有1张会中奖；
（6）函数与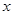轴必有两个交点．

A．2

B．3

C．4

D．5

如图，正方形ABCD中，AB=8cm,对角线AC,BD相交于点O,点E,F分别从B,C两点同时出发，以1cm/s的速度沿BC,CD运动，到点C,D时停止运动，设运动时间为t（s）,△OEF的面积为s（），则s（）与t（s）的函数关系可用图像表示为（）

如图，已知点A（4，0），O为坐标原点，P是线段OA上任意一点（不含端点O，A），过P、O两点的二次函数y₁和过P、A两点的二次函数y₂的图象开口均向下，它们的顶点分别为B、C，射线OB与AC相交于点D．当OD=AD=3时，这两个二次函数的最大值之和等于（）

A． B． C．3 D．4

如图，Rt△ABC中，AC=BC=2，正方形CDEF的顶点D.F分别在AC.BC边上，设CD的长度为x，△ABC与正方形CDEF重叠部分的面积为y，则下列图象中能表示y与x之间的函数关系的是（）

小李从如图所示的二次函数y=ax²+bx+c（a≠0）的图象中，观察得出了下面四条信息：①b²﹣4ac＞0；②c＞1；③ab＞0；④a﹣b+c＜0．你认为其中正确的有（）．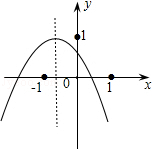

A．1个

B．2个

C．3个

D．4个

已知M、N两点关于y轴对称，且点M在双曲线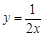上，点N在直线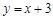上，设点M的坐标为（a，b），则二次函数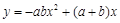

A．有最大值－4．5	B．有最大值4．5
C．有最小值4．5	D．有最小值－4．

若函数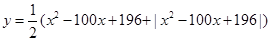，则当自变量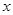取1、2、3、…、100这100个自然数时，函数值的和是（）。

A．540

B．390

C．194

D．97

如图，△ABC中，∠ACB=90°，∠A=30°，AB=16．点P是斜边AB上一点．过点P作PQ⊥AB，垂足为P，交边AC（或边CB）于点Q，设AP=x，△APQ的面积为y，则y与x之间的函数图象大致为（）

已知函数y=|（x﹣1）²﹣1|，则使y=k成立的x值恰好有三个，则k的值为（）

A．0

B．1

C．2

D．3

如图，直线y=kx+c与抛物线y=ax²+bx+c的图象都经过y轴上的D点，抛物线与x轴交于A、B两点，其对称轴为直线x=1，且OA=OD．直线y=kx+c与x轴交于点C（点C在点B的右侧）．则下列命题中正确命题的个数是（）
①abc＞0；②3a+b＞0；③﹣1＜k＜0；④k＞a+b；⑤ac+k＞0．

A．1 B．2 C．3 D．4

如图，正方形ABCD的边长为3cm，动点P从B点出发以3cm/s的速度沿着边BC-CD-DA运动，到达A点停止运动；另一动点Q同时从B点出发，以1cm/s的速度沿着边BA向A点运动，到达A点停止运动．设P点运动时间为x（s），△BPQ的面积为y（cm²），则y关于x的函数图象是（）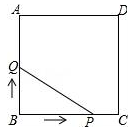

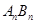对于每个非零自然数n，抛物线与x轴交于A_n、B_n两点，以表示这两点间的距离，则的值是（ ）

A．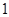

B．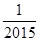

C．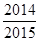

D．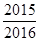

如图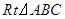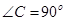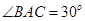，，，，AB=8，以为边长的正方形DEFG的一边GD在直线AB上，且点D与点A重合．现将正方形DEFG沿A→B的方向以每秒1个单位的速度匀速运动，当点D与点B重合时停止，则在这个运动过程中，正方形DEFG与⊿ABC的重合部分的面积与运动时间之间的函数关系图像大致是（）

如图，在平面直角坐标系中，抛物线经过平移得到抛物线，其对称轴与两段抛物线所围成的阴影部分的面积是（）

A．2

B．4

C．8

D．16