如图1,过△ABC的三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC的“水平宽(a)”,中间的这条直线在△ABC内部的线段的长度叫△ABC的“铅垂高(h)”.我们可得出一种计算三角形面积的新方法:S△ABC= ah,即三角形的面积等于水平宽与铅垂高乘积的一半.
ah,即三角形的面积等于水平宽与铅垂高乘积的一半.
解答问题:
如图2,顶点为C(1,4)的抛物线y=ax2+bx+c交x轴于点A(3,0)、交y轴于点B.
(1)求抛物线和直线AB的解析式.
(2)点P是抛物线(在第一象限内)上的一个动点,连接PA、PB.
①当P点运动到顶点C时,求△CAB的铅垂高CD及S△CAB.
②是否存一点P,使S△PAB= S△CAB?若存在,求出点P的坐标;若不存在,请说明理由.
S△CAB?若存在,求出点P的坐标;若不存在,请说明理由.
已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且|OC|=3|OA|
(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
已知抛物线
(1)填空:抛物线的顶点坐标是( , ),对称轴是 ;
(2)已知y轴上一点A(0,-2),点P在抛物线上,过点P作PB⊥x轴,垂足为B.若△PAB是等边三角形,求点P的坐标;
(3)在(2)的条件下,点M在直线AP上.在平面内是否存在点N,使以点O、点A、点M、点N为顶点的四边形为菱形?若存在,直接写出所有满足条件的点N的坐标;若不存在,请说明理由.

如图,平面直角坐标系 中,
中, 为坐标原点,抛物线
为坐标原点,抛物线 交x轴于A、B两点(点A在点B的左侧),交y轴于点C,以OB、OC为边作矩形OBDC,CD交抛物线于G.
交x轴于A、B两点(点A在点B的左侧),交y轴于点C,以OB、OC为边作矩形OBDC,CD交抛物线于G.
(1)求OB和OC的长;
(2)抛物线的对称轴在边OB(不包括O、B两点)上作平行移动,交x轴于点E,交CD于点F,交BC于点M,交抛物线于点P.设OE=m,PM=h,求h与m的函数关系式,并求PM的最大值;
(3)连接PC,在CD上方的抛物线部分是否存在这样的点P,使得以P、C、F为顶点的三角形与△BEM相似?若存在,求出相应的m的值,并判断△PCM的形状;若不存在,请说明理由.
已知,如图,抛物线 >0)与
>0)与 轴交于点C,与
轴交于点C,与 轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
轴交于A,B两点,点A在点B左侧.点B的坐标为(1,0),OC=3OB.
(1)求抛物线的解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值;
(3)若点E在 轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
轴上,点P在抛物线上.是否存在以A,C,E,P为顶点且以AC为一边的平行四边形?若存在,直接写出点P的坐标;若不存在,请说明理由.
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐助给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量 (单位:个)与销售单价
(单位:个)与销售单价 (单位:元/个)之间的对应关系如图所示:
(单位:元/个)之间的对应关系如图所示:

(1) 与
与 之间的函数关系是 .
之间的函数关系是 .
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润 (单位:元)与销售单价
(单位:元)与销售单价 (单位:元/个)之间的函数关系式;
(单位:元/个)之间的函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ,
, )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)求△PAC为直角三角形时点P的坐标.
如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A( ,
, )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由.
山西特产专卖店销售核桃,其进价为每千克40元,按每千克60元出售,平均每天可售出100千克,后来经过市场调查发现,单价每降低2元,则平均每天的销售可增加20千克,若该专卖店销售这种核桃要想平均每天获利2240元,请回答:
(1)每千克核桃应降价多少元?
(2)在(1)问的条件下,平均每天获利不变,为尽可能让利于顾客,赢得市场,该店应按原售价的几折出售?
(3)写出每天总利润 与降价
与降价 元的函数关系式,为了使每天的利润最大,应降价多少元?
元的函数关系式,为了使每天的利润最大,应降价多少元?
如图,抛物线y=ax2+bx+c经过原点,与x轴相交于点E(8,0),抛物线的顶点A在第四象限,点A到x轴的距离AB=4,点P(m,0)在线段OB上,连结PA,将线段PA绕点P逆时针旋转90°得到线段PC,过点C作y轴的平行线交x轴于点G,交抛物线于点D,连结BC和AD.
(1)求抛物线的解析式;
(2)求点C的坐标(用含m的代数式表示);
(3)当四边形ABCD是平行四边形时,求点P的坐标.
如图,抛物线y= x2-
x2- x-12与x轴交于A、C两点,与y轴交于B点.
x-12与x轴交于A、C两点,与y轴交于B点.
(1)求△AOB的外接圆的面积;
(2)若动点P从点A出发,以每秒2个单位沿射线AC方向运动;同时,点Q从点B出发,以每秒1个单位沿射线BA方向运动,当点P到达点C处时,两点同时停止运动。问当t为何值时,以A、P、Q为顶点的三角形与△OAB相似?
(3)若M为线段AB上一个动点,过点M作MN平行于y轴交抛物线于点N.
①是否存在这样的点M,使得四边形OMNB恰为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
②当点M运动到何处时,四边形CBNA的面积最大?求出此时点M的坐标及四边形CBAN面积的最大值.
如图,在△ABC中,AB=5,AC=9,S△ABC=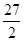 ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.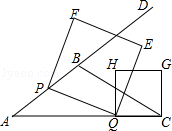
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
如图,边长为8的正方形OABC的两边在坐标轴上,以点C为顶点的抛物线经过点A,点P是抛物线上点A、C间的一个动点(含端点),过点P作PF⊥BC于点F.点D、E的坐标分别为(0,6),(-4,0),连接PD,PE,DE.

(1)请直接写出抛物线的解析式;
(2)小明探究点P的位置发现:当点P与点A或点C重合时,PD与PF的差为定值.进而猜想:对于任意一点P,PD与PF的差为定值.请你判断该猜想是否正确,并说明理由
(3)小明进一步探究得出结论:若将“使△PDE的面积为整数”的点P记作“好点”,
①请直接写出所有“好点”的个数,
②如果使△PDE的周长最小的点P也是一个“好点”,请求出△PDE的周长最小时“好点”的坐标.
已知:如图,抛物线 与
与 轴交于点A(-1,0),B(3,0),与
轴交于点A(-1,0),B(3,0),与 轴交于点C.过点C作CD∥
轴交于点C.过点C作CD∥ 轴,交抛物线的对称轴于点D.
轴,交抛物线的对称轴于点D.
(1)求该抛物线的解析式;
(2)若将该抛物线向下平移m个单位,使其顶点落在D点,求m的值.
试题篮
()