初中数学二次函数在给定区间上的最值解答题

综合与探究：
如图，抛物线y=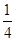x²-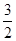x-4与x轴交与A，B两点（点B在点A的右侧），与y轴交于点C，连接BC，以BC为一边，点O为对称中心作菱形BDEC，点P是x轴上的一个动点，设点P的坐标为（m，0），过点P作x轴的垂线l交抛物线于点Q．
（1）求点A，B，C的坐标．
（2）当点P在线段OB上运动时，直线l分别交BD，BC于点M，N．试探究m为何值时，四边形CQMD是平行四边形，此时，请判断四边形CQBM的形状，并说明理由．
（3）当点P在线段EB上运动时，是否存在点Q，使△BDQ为直角三角形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．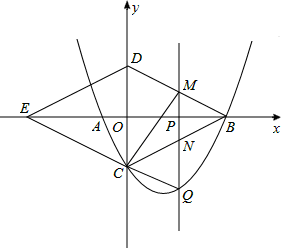

已知：如图1，抛物线的顶点为M，平行于x轴的直线与该抛物线交于点A，B（点A在点B左侧），根据对称性△AMB恒为等腰三角形，我们规定：当△AMB为直角三角形时，就称△AMB为该抛物线的“完美三角形”．

（1）①如图2，求出抛物线的“完美三角形”斜边AB的长；
②抛物线与的“完美三角形”的斜边长的数量关系是；
（2）若抛物线的“完美三角形”的斜边长为4，求a的值；
（3）若抛物线的“完美三角形”斜边长为n，且的最大值为-1，求m，n的值．

如图，经过原点的抛物线y=-x²+bx（b＞2）与x轴的另一交点为A，过点P（1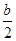，）作直线PN⊥x轴于点N，交抛物线于点B．点B关于抛物线对称轴的对称点为C．连结CB，CP．
（1）当b=4时，求点A的坐标及BC的长；
（2）连结CA，求b的适当的值，使得CA⊥CP；
（3）当b=6时，如图2，将△CBP绕着点C按逆时针方向旋转，得到△CB′P′，CP与抛物线对称轴的交点为E，点M为线段B′P′（包含端点）上任意一点，请直接写出线段EM长度的取值范围．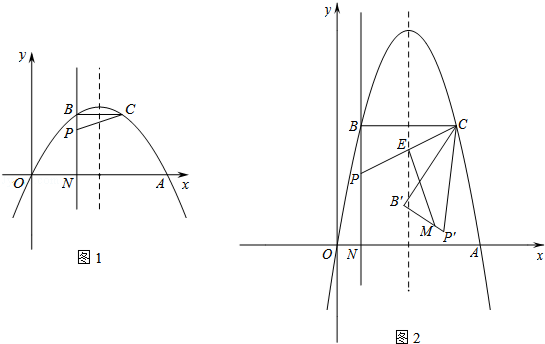

如图，点A（-2，5）和点B（-5，a）在反比例函数y=的图象上，直线y=x+b分别交x轴的正半轴于点D，交y轴的负半轴于点C，且AB=CD．二次函数的图象经过A、C、D三点．

（1）求a、k的值及直线AB的函数表达式；
（2）求点C、D的坐标及二次函数的表达式；
（3）如果点E在第四象限的二次函数图象上，且∠OCE=∠BDC，求点E的坐标．

如图，抛物线y=ax²+x+c与x轴交于点A（4，0）、B（-1，0），与y轴交于点C，连接AC，点M是线段OA上的一个动点（不与点O、A重合），过点M作MN∥AC，交OC于点N，将△OMN沿直线MN折叠，点O的对应点O′落在第一象限内，设OM=t，△O′MN与梯形AMNC重合部分面积为S．
（1）求抛物线的解析式；
（2）①当点O′落在AC上时，请直接写出此时t的值；
②求S与t的函数关系式；
（3）在点M运动的过程中，请直接写出以O、B、C、O′为顶点的四边形分别是等腰梯形和平行四边形时所对应的t值．

（本小题满分10分）设抛物线与x轴交于两个不同的点A（一1，0）B（4，0），与y轴交于点C．

（1）求抛物线的解析式及∠ACB的度数；
（2）已知点D（1，n ）在抛物线上，过点A的直线交抛物线于另一点E．若点P在x轴上，以点P、B、D为顶点的三角形与△AEB相似，求点P的坐标．

如图，二次函数y=ax²+bx（a＜0）的图象过坐标原点O，与x轴的负半轴交于点A，过A点的直线与y轴交于B，与二次函数的图象交于另一点C，且C点的横坐标为﹣1，AC：BC=3：1．
（1）求点A的坐标；
（2）设二次函数图象的顶点为F，其对称轴与直线AB及x轴分别交于点D和点E，若△FCD与△AED相似，求此二次函数的关系式．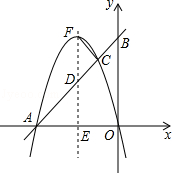

为了贯彻落实市委市府提出的“精准扶贫”精神．某校特制定了一系列关于帮扶A、B两贫困村的计划．现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如下表：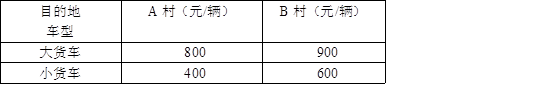

（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．

在平面直角坐标系中，二次函数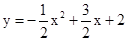的图像与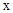轴交于点A，B（点B在点A的左侧），与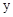轴交于点C，过动点H（0, 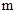）作平行于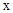轴的直线，直线与二次函数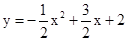的图像相交于点D，E.
（1）写出点A,点B的坐标；
（2）若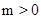，以DE为直径作⊙Q，当⊙Q与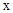轴相切时，求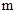的值；
（3）直线上是否存在一点F，使得△ACF是等腰直角三角形？若存在，求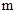的值；若不存在，请说明理由.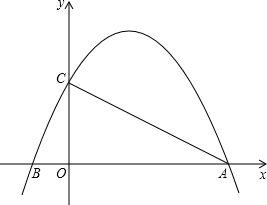

如图，在直角坐标系中，A点在x轴上，AB∥y轴，C点在y轴上，CB∥x轴，点B的坐标为（8，10），点D在BC上，将△ABD沿直线AD翻折，使得点B刚好落在y轴的点E处．

（1）求△CDE的面积；
（2）求经过A、D、O三点的抛物线的解析式；
（3）点M是（2）中抛物线上的动点,点N是其对称轴上的动点,问是否存在这样的点M和点N,使得以A、E、M、N为顶点的四边形是平行四边形？若存在,请直接写出点M和点N的坐标;若不存在,请说明理由．

抛物线y=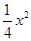+x+m的顶点在直线y=x+3上，过点F（-2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．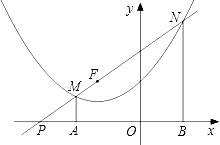

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；
（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；
（3）若射线NM交x轴于点P，且PA•PB=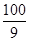，求点M的坐标．

已知，抛物线y=ax²+bx+4（a≠0）与x轴交于A（﹣2，0）、B（8，0）两点，与y轴交于点C．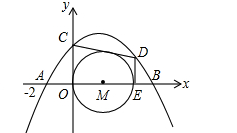

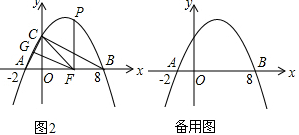
（1）求此抛物线的解析式；
（2）如图1，点E是线段OB上一动点，过点E作DE⊥x轴，交抛物线于点D，若直线CD与以OE为直径的⊙M相切，试求出点E的坐标；
（3）如图2，在抛物线上是否存在一点P，过点P作x轴的垂线，垂足为F，过点F作FG∥BC，交线段AC于点G，连接FC，使△BCF∽△CFG？若存在，求出点P的坐标；若不存在，请说明理由．

已知二次函数y=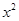+bx+c的图象如图所示，它与x轴的一个交点的坐标为（－1，0），与y轴的交点坐标为（0，－3）．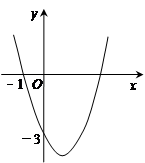

（1）求此二次函数的解析式；
（2）求此二次函数的图象与x轴的另一个交点的坐标；
（3）根据图象回答：当x取何值时，y＜0？

某体育用品商店为了解8月份的销售情况，对本月各类商品的销售情况进行调查，并将调查的结果绘制成如下的两幅不完整的统计图．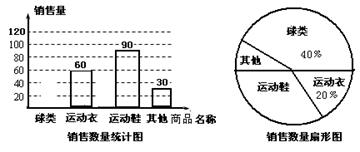

（1）请根据图中提供的信息，将条形图补充完整；
（2）该商店准备按8月份球类商品销量的数量购进球类商品，含篮球、足球、排球三种
球，预计恰好用完货款共3600元.设购进篮球x个，足球y个，三种球的进价和售
价如下表：

类别	篮球	足球	排球
进价（单位：元/个）	50	30	20
预售价（单位：元/个）	70	45	25

求出y与x之间的函数关系式；
（3）在（2）中的进价和售价的条件下，据实际情况，预计足球销售超过60个后，这种
球就会产生滞销，①假设所购进篮球、足球、排球能全部售出，求出预估利润P（元）与x（个）的函数关系式；②求出预估利润的最大值，并写出此时购进三种球各多少个？

如图，已知点A（3，0），以A为圆心作⊙A与Y轴切于原点，与x轴的另一个交点为B，过B作⊙A的切线l．

（1）以直线l为对称轴的抛物线过点A及点C（0，9），求此抛物线的解析式；
（2）抛物线与x轴的另一个交点为D，过D作⊙A的切线DE，E为切点，求DE的长；
（3）点F是切线DE上的一个动点，当△BFD与△EAD相似时，求出BF的长 ．