如图,在平面直角坐标系中,已知OA=2,OC=4,⊙M与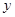 轴相切于点C,与
轴相切于点C,与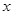 轴交于A,B两点,∠ACD=90°,抛物线
轴交于A,B两点,∠ACD=90°,抛物线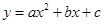 经过A,B,C三点.
经过A,B,C三点.
(1)求证:∠CAO=∠CAD;
(2)求弦BD的长;
(3)在抛物线的对称轴上是否存在点P使ΔPBC是以BC为腰的等腰三角形?若存在,求出点P的坐标;若不存在,请说明理由.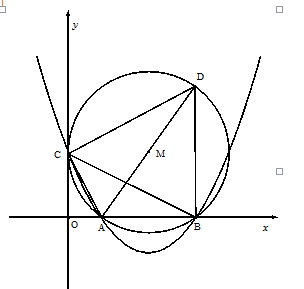
如图,在平面直角坐标系xOy中,抛物线 过点
过点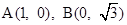 ,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=
,这条抛物线的对称轴与x轴交于点C,点P为射线CB上一个动点(不与点C重合),点D为此抛物线对称轴上一点,且CPD=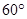 .
.
(1)求抛物线的解析式;
(2)若点P的横坐标为m,△PCD的面积为S,求S与m之间的函数关系式;
(3)过点P作PE⊥DP,连接DE,F为DE的中点,试求线段BF的最小值.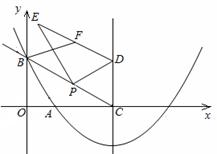
如图①,在□ABCD中,对角线AC⊥AB,BC=10,tan∠B=2.点E是BC边上的动点,过点E作EF⊥BC于点E,交折线AB-AD于点F,以EF为边在其右侧作正方形EFGH,使EH边落在射线BC上.点E从点B出发,以每秒1个单位的速度在BC边上运动,当点E与点C重合时,点E停止运动,设点E的运动时间为t(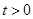 )秒.
)秒.
(1)□ABCD的面积为 ;当t= 秒时,点F与点A重合;
(2)点E在运动过程中,连接正方形EFGH的对角线EG,得△EHG,设△EHG与△ABC的重叠部分面积为S,请直接写出S与t的函数关系式以及对应的自变量t的取值范围;
(3)作点B关于点A的对称点Bˊ,连接CBˊ交AD边于点M(如图②),当点F在AD边上时,EF与对角线AC交于点N,连接MN得△MNC.是否存在时间t,使△MNC为等腰三角形?若存在,请求出使△MNC为等腰三角形的时间t;若不存在,请说明理由.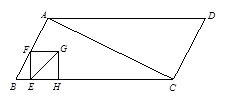
如图1,□ABCD中,对角线BD⊥AB,AB=5,AD边上的高为 .等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
.等腰直角△EFG中,EF=4, ∠EGF=45°,且△EFG与□ABCD位于直线AD的同侧,点F与点D重合,GF与AD在同一直线上.△EFG从点D出发以每秒1个单位的速度沿射线DA方向平移,当点G到点A时停止运动;同时点P也从点A出发,以每秒3个单位的速度沿折线AD→DC方向运动,到达点C时停止运动,设运动的时间为t.
(1)求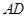 的长度;
的长度;
(2)在 平移的过程中,记
平移的过程中,记 与
与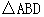 相互重叠的面积为
相互重叠的面积为 ,请直接写出面积
,请直接写出面积 与运动时间
与运动时间 的函数关系式,并写出
的函数关系式,并写出 的取值范围;
的取值范围;
(3)如图2,在运动的过程中,若线段 与线段
与线段 交于点
交于点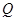 ,连接
,连接 .是否存在这样的时间
.是否存在这样的时间 ,使得
,使得 为等腰三角形?若存在,求出对应的
为等腰三角形?若存在,求出对应的 值;若不存在,请说明理由.
值;若不存在,请说明理由.

如图,在矩形ABCD中,AB=1,BC=3,点E为BC边上的动点(点E与点B、C不重合),设BE=x.
操作:在射线BC上取一点F,使得EF=BE,以点F为直角顶点、EF为边作等腰直角三角形EFG,设△EFG与矩形ABCD重叠部分的面积为S.
(1)求S与x的函数关系式,并写出自变量x的取值范围;
(2)S是否存在最大值?若存在,请直接写出最大值,若不存在,请说明理由.
如图,在平面直角坐标系中,△ABC的边AB在x轴上,∠ABC=90°,AB=BC,OA=1,OB=4,抛物
线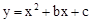 经过A、C两点.
经过A、C两点.
(1)求抛物线的解析式及其顶点坐标;
(2)如图①,点P是抛物线上位于x轴下方的一点,点Q与点P关于抛物线的对称轴对称,过点P、Q分别向x轴作垂线,垂足为点D、E,记矩形DPQE的周长为d,求d的最大值,并求出使d最大值时点P的坐标;
(3)如图②,点M是抛物线上位于直线AC下方的一点,过点M作MF⊥AC于点F,连接MC,作MN∥BC交直线AC于点N,若MN将△MFC的面积分成2:3两部分,请确定M点的坐标.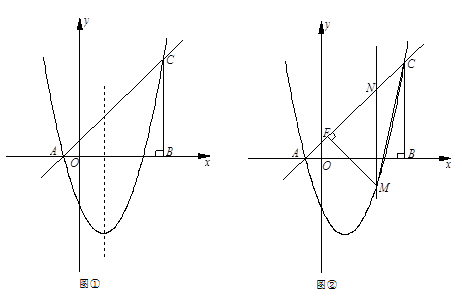
如图,在直角坐标平面内,O为原点,抛物线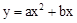 经过点A(6,0),且顶点B(m,6)在直线
经过点A(6,0),且顶点B(m,6)在直线 上.
上.
(1)求m的值和抛物线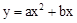 的解析式;
的解析式;
(2)如在线段OB上有一点C,满足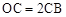 ,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
,在x轴上有一点D(10,0),连接DC,且直线DC与y轴交于点E.
①求直线DC的解析式;
②如点M是直线DC上的一个动点,在x轴上方的平面内有另一点N,且以O、E、M、N为顶点的四边形是菱形,请直接写出点N的坐标.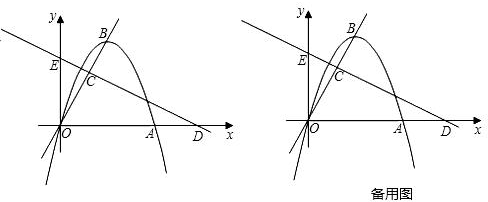
如图,在平面直角坐标系xOy中,点A(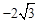 ,0),点B(0,2),点C是线段OA的中点.
,0),点B(0,2),点C是线段OA的中点.
(1)点P是直线AB上的一个动点,当PC+PO的值最小时,
①画出符合要求的点P(保留作图痕迹);
②求出点P的坐标及PC+PO的最小值;
(2)当经过点O、C的抛物线y=ax2+bx+c与直线AB只有一个公共点时,求a的值并指出这个公共点所在象限.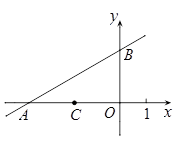
如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+n与x轴、y轴分别交于B、C两点,抛物线y=ax2+bx+3(a≠0)过C、B两点,交x轴于另一点A,连接AC,且tan∠CAO=3.
(1)求抛物线的解析式;
(2)若点P是射线CB上一点,过点P作x轴的垂线,垂足为H,交抛物线于Q,设P点横坐标为t,线段PQ的长为d,求出d与t之间的函数关系式,并写出相应的自变量t的取值范围;
(3)在(2)的条件下,当点P在线段BC上时,设PH=e,已知d,e是以y为未知数的一元二次方程:y2-(m+3)y+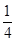 (5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.
(5m2-2m+13)="0" (m为常数)的两个实数根,点M在抛物线上,连接MQ、MH、PM,且.MP平分∠QMH,求出t值及点M的坐标.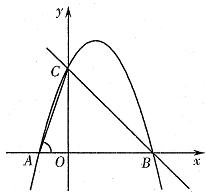
如图,在平面直角坐标系中,已知点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(点P与F、G不重合),作PQ∥y轴与抛物线交于点Q.
(1)若经过B、E、C三点的抛物线的解析式为y=-x2+(2b-1)x+c-5,则b= ,c= (直接填空)
(2)①以P、D、E为顶点的三角形是直角三角形,则点P的坐标为 (直接填空)
②若抛物线顶点为N,又PE+PN的值最小时,求相应点P的坐标.
(3)连结QN,探究四边形PMNQ的形状:
①能否成为平行四边形
②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.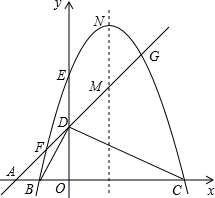
如图1,在菱形ABCD中,对角线AC、BD相交于点O,AC=8,BD=6.现有两动点P、Q分别从A、C两点同时出发,点P以每秒1个单位长的速度由点A向点D做匀速运动,点Q沿折线CB—BA向点A做匀速运动.
(1)点P将要运行路径AD的长度为 ;点Q将要运行的路径折线CB—BA的长度为 .
(2)当点Q在BA边上运动时,若点Q的速度为每秒2个单位长,设运动时间为t秒.
①求△APQ的面积S关于t的函数关系式,并求自变量t的取范围;
②求当t为何值时,S有最大值,最大值是多少?
(3)如图2,若点Q的速度为每秒a个单位长(a≤ ),当t =4秒时:
),当t =4秒时:
①此时点Q是在边CB上,还是在边BA上呢?
②△APQ是等腰三角形,请求出a的值.
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=90°,且EF交正方形外角的平分线CF于点F.
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线y=-x2+x+1上,求此时点F的坐标.
如图1,已知A(3,0)、B(4,4)、原点O(0,0)在抛物线y=ax2+bx+c (a≠0)上.

(1)求抛物线的解析式.
(2)将直线OB向下平移m个单位长度后,得到的直线与抛物线只有一个交点D,求m的值及点D的坐标.
(3)如图2,若点N在抛物线上,且∠NBO=∠ABO,则在(2)的条件下,求出所有满足△POD∽△NOB的点P的坐标(点P、O、D分别与点N、O、B对应)
如图,在平面直角坐标系中,点A坐标为(-2,0),点B坐标为(0,2),点E为线段AB上的动点(点E不与点A,B重合),以E为顶点作∠OET=45°,射线ET交线段OB于点F,C为y轴正半轴上一点,且OC=AB,抛物线y=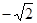 x2+mx+n的图象经过A,C两点.
x2+mx+n的图象经过A,C两点.
(1)求此抛物线的函数表达式;
(2)求证:∠BEF=∠AOE;
(3)当△EOF为等腰三角形时,求此时点E的坐标;
(4)在(3)的条件下,当直线EF交x轴于点D,P为(1)中抛物线上一动点,直线PE交x轴于点G,在直线EF上方的抛物线上是否存在一点P,使得△EPF的面积是△EDG面积的(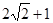 )倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
)倍.若存在,请直接写出点P坐标;若不存在,请说明理由.
如图,直线y=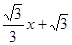 与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点
与x轴交于点A,与y轴交于点C,以AC为直径作⊙M,点 是劣弧AO上一动点(
是劣弧AO上一动点( 点与
点与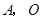 不重合).抛物线y=-
不重合).抛物线y=-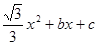 经过点A、C,与x轴交于另一点B,
经过点A、C,与x轴交于另一点B,
(1)求抛物线的解析式及点B的坐标;
(2)在抛物线的对称轴上是否存在一点P,是︱PA—PC︱的值最大;若存在,求出点P的坐标;若不存在,请说明理由。
(3)连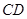 交
交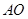 于点
于点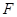 ,延长
,延长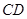 至
至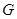 ,使
,使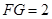 ,试探究当点
,试探究当点 运动到何处时,直线
运动到何处时,直线 与⊙M相切,并请说明理由.
与⊙M相切,并请说明理由.
试题篮
()