下列图形都是由同样大小的正方形和正三角形按一定的规律组成,其中,第①个图形中一共有5个正多边形,第②个图形中一共有13个正多边形,第③个图形中一共有26个正多边形,……,则第⑥个图形中正多边形的个数为( )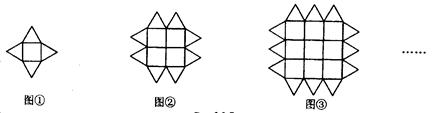
| A.90 | B.91 | C.115 | D.116 |
将一张等边三角形纸片按图1-①所示的方式对折,再按图1-②所示的虚线剪去一个小三角形,将余下纸片展开得到的图案是 ( )

下面每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n(n≥2)个圆点时,图案的圆点数为Sn,按此规律推算Sn 关于n的关系式为:__________________.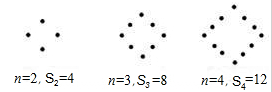
用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n个图案中正三角形的个数为 (用含n的代数式表示).
平面直角坐标系中,O为坐标原点,点A的坐标为(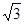 ,1),将OA绕原点按逆时针方向旋转30°得OB,则点B的坐标为【 】
,1),将OA绕原点按逆时针方向旋转30°得OB,则点B的坐标为【 】
A.(1,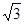 ) ) |
B.( -1,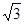 ) ) |
C.(0,2) | D.(2,0) |
如图,由等圆组成的一组图中,第1个图由1个圆组成,第2个图由5个圆组成,第3个图由11个圆组成,……,按照这样的规律排列下去,则第9个图形由_______个圆组成,第n个图形由________个圆组成。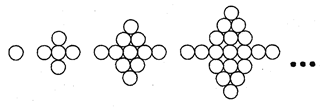
阅读下列材料:
在学习小组,小明接到这样一个任务:把一个正方形分割成9个、10个和11个小正方形。为完成任务,小明先学习了两种简单的“基本分割法”。
基本分割法1:如图①,把一个正方形分割成4个小正方形,即在原来1个正方形的基础上增加了3个正方形.
基本分割法2:如图②,把一个正方形分割成6个小正方形,即在原来1个正方形的基础上增加了5个正方形.
学习了上述两种“基本分割法”后,小明很从容地就完成了分割的任务:
(1)把一个正方形分割成9个小正方形.
方法一:如图③,把图①中的任意1个小正方形按“基本分割法2”进行分割,就可增加5个小正方形,从而分割成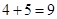 (个)小正方形.
(个)小正方形.
方法二:如图④,把图②中的任意1个小正方形按“基本分割法1”进行分割,就可增加3个小正方形,从而分割成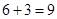 (个)小正方形.
(个)小正方形.
(2)把一个正方形分割成10个小正方形.
如图⑤,把图①中的任意2个小正方形按“基本分割法1”进行分割,就可增加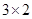 个小正方形,从而分割成
个小正方形,从而分割成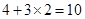 (个)小正方形.
(个)小正方形.
请你参照上述分割方法解决下列问题(只要求画图,不用说明分割方法):
(1)请你替小明同学把图⑥给出的正方形分割成11个小正方形;
(2)仿照基本分割法1:请把图a中的正三角形分割成4个小正三角形;
(3)仿照基本分割法2:请把图b 中的正三角形分割成6个小正三角形;
(4)分别把图c和图d中的正三角形分割成9个和10个小正三角形.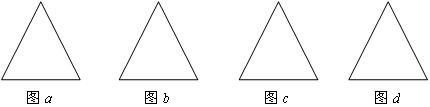
把一张正方形纸片按如图所示对折两次后,再挖去一个小圆孔,那么展开后的图形应为( )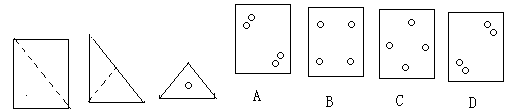
某餐厅中,一张桌子可坐6人,有以下两种摆放方式:
(1)当有n张桌子时,两种摆放方式各能坐多少人?
(2)一天中午餐厅要接待98位顾客共同就餐,但餐厅只有25张这样的餐桌,若你是这个餐厅的经理,你打算选择哪种方式来摆放餐桌?为什么?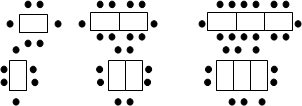
试题篮
()