已知△ABC的三边分别为m2-n2,2mn,m2+n2(m,n为正整数,且m>n),求证:△ABC是直角三角形.
若直角三角形两直角边的比是3:4,斜边长是20cm,则直角三角形的面积是________.
如图AB=AC,则数轴上点C所表示的数为( )
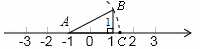
A.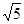 +1 +1 |
B.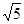 -1 -1 |
C.- +1 +1 |
D.-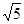 -1 -1 |
等腰Rt△ABC中,∠BAC=90°,点A、点B分别是x轴、y轴两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;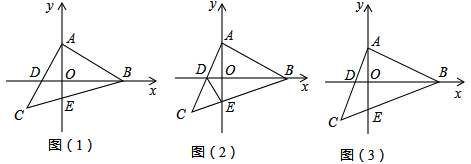
(1)如图(1),若A(0,1),B(2,0),求C点的坐标;
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE
(3)如图(3),在等腰Rt△ABC不断运动的过程中,若满足BD始终是∠ABC的平分线,试探究:线段OA、OD、BD三者之间是否存在某一固定的数量关系,并说明理由.
如图,在等腰Rt△ABC中,∠ACB=90o,AC=CB,F是AB边上的中点,点D、E分别在AC、BC边上运动,且始终保持AD=CE,连接DE、DF、EF.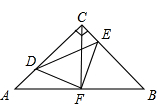
(1)求证:△ADF≌△CEF;
(2)试证明△DFE是等腰直角三角形.
如图,在△ABC中,AB=AC,D是BC边上的一点,DE⊥AB,DF⊥AC,垂足分别为E、F,添加一个条件,使DE= DF,并说明理由.
解: 需添加条件是 .

理由是:
在△ABC中, AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.
(1)求证: ;
;
(2)若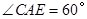 ,求
,求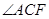 的度数.
的度数.
如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,求证:BD=ED.
如图,∠BAC=∠ABD,AC=BD,点O是AD、BC的交点,点E是AB的中点.试判断OE和AB的位置关系,并给出证明.
如图,某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=____海里.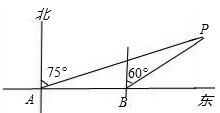
在△ABC中,已知点D,E,F分别是BC、AD、CE的中点,且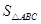 =4cm2,则
=4cm2,则 =_______cm2.
=_______cm2.
如图,已知AB=AD,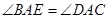 ,要使
,要使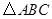 ≌
≌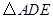 ,若以“SAS”为依据,补充的条件是 .
,若以“SAS”为依据,补充的条件是 .

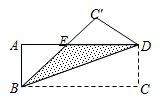
如图,把一张矩形纸片ABCD沿对角线BD折叠,使C点落在C',且BC'与AD交于E点,若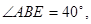 则
则 °
°
如图,在△ABC中,AB=AC,AD⊥BC于D点,E、F分别为DB、DC的中点,则图中共有全等三角形 对.

试题篮
()