初中数学三角形的五心选择题

如图，等边三角形ABC的边长为3，点P为BC边上一点，且BP=1，点D为AC边上一点，若∠APD=60°，则CD的长为

A．

B．

C．

D．1

下列判断中错误的是（     ）．
A．有两角和一边对应相等的两个三角形全等
B．有两边和一角对应相等的两个三角形全等
C．有两边和其中一边上的中线对应相等的两个三角形全等

如图，已知△ABC中，∠ABC=45°，F是高AD和BE的交点，CD=4，则线段DF的长度为(    )

A．

B．4

C．

D．

△ABC的周长为30 cm，把△ABC的边AC对折，使顶点C和点A重合，折痕交BC边于点D，交AC边于点E，连接AD，若AE=4cm，则△ABD的周长是

A．22cm

B．20cm

C．18cm

D．15cm

在下列各组条件中，不能说明△ABC≌△DEF的是（ ）

A．AB=DE，∠B=∠E，∠C=∠F

B．AC=DF，BC=EF，∠A=∠D

C．AB=DE，∠A=∠D，∠B=∠E

D．AB=DE，BC=EF，AC=DF

用直尺和圆规作一个角等于已知角，如图，能得出∠A′O′B′=∠AOB的依据是（ ）

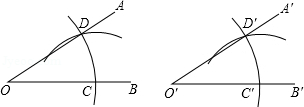
A．（SAS）   B．（SSS）    C．（ASA）    D．（AAS）

把一块直尺与一块三角板如图放置，若∠1=40°，则∠2的度数为（ ）

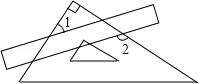
A．125°

B．120°

C．140°

D．130°

如图，C为线段AE上一动点（不与点A，E重合），在AE同侧分别作等边△ABC和等边△CDE，AD与BE交于点O，AD与BC交于点P，BE与CD交于点Q，连接PQ．以下五个结论：

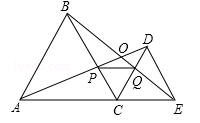
①AD=BE；②PQ∥AE；③AP=BQ；④DE=DP； ⑤∠AOB=60°．
其中正确的结论的个数是（   ）

A．2个

B．3个

C．4个

D．5个

已知AD是△ABC的中线，BE是△ABD的中线，若△ABC的面积为20，则△ABE的面积为（   ）

A．5

B．10

C．15

D．18

如图，将△ABC沿直线DE折叠后，使得点B与点A重合．已知AC=5cm，△ADC的周长为17cm，则BC的长为（ ）

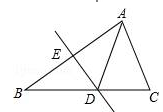
A．7cm

B．10cm

C．12cm

D．22cm

如图，△ABC中，AB=AC，D为BC的中点，以下结论：
（1）△ABD≌△ACD；（2）AD⊥BC；（3）∠B=∠C；（4）AD是△ABC的角平分线．
其中正确的有（ ）

A．1个

B．2个

C．3个

D．4个

如图是一个风筝设计图，其主体部分（四边形ABCD）关于BD所在的直线对称，AC与BD相交于点O，且AB≠AD，则下列判断不正确的是（   ）

A．AC垂直平分BD   
B．△ABD≌△CBD 
C．△AOB≌△COB 
D．△AOD≌△COD

以下列各组数据作为三边长，能组成直角三角形的是（ ）

A．1，2，3

B．2，3，4

C．3，4，5

D．4，5，6

如图，平行四边形ABCD中，E，F是对角线BD上的两点，如果添加一个条件使△ABE≌△CDF，则添加的条件不能是（ ）

A．AE=CF

B．BE=FD

C．BF=DE

D．∠1=∠2

下面四个图形中，线段BE是⊿ABC的高的图是（     ）