初中数学三角形的五心试题

直角三角形两条边长分别是5和12，则第三边上的中线长是           ．

已知△ABC的三边长a、b、c，化简|a+b﹣c|﹣|b﹣a﹣c|的结果是     ．

下列四组线段中，能组成三角形的是（ ）

A．2cm，3cm，4cm	B．3cm，4cm，7cm
C．4cm，6cm，2cm	D．7cm，10cm，2cm

如图，已知一张长方形纸片ABCD，AB∥CD ，AD=BC=1，AB=CD=5．在长方形ABCD的边AB上取一点M，在CD上取一点N，将纸片沿MN折叠，使MB与DN交于点K，得到△MNK．

（1）请你动手操作，判断△MNK的形状一定是                  ；
（2）问△MNK的面积能否小于？试说明理由；
（3）如何折叠能够使△MNK的面积最大？请你用备用图探究可能出现的情况，并求最大值．

如图，在等腰三角形ABC中，∠ABC=90°，D为AC边上中点，过D点作DE⊥DF，交AB于E，交BC于F．请解答下列问题：

（1）连结BD，试说明∠BDE=∠CDF；
（2）求证：BE=FC；
（2）若AE=4，FC=3，求EF长．

某航船以20海里/时的速度向正北方向航行，在A处看灯塔Q在航船北偏东45°处，半小时后航行到B处，此时灯塔Q与航船的距离最短．

（1）请你在图中画出点B的位置；
（2）求灯塔Q到A处的距离．（精确到0．1海里）

如图，点B、F、C、E在同一直线上，∠A=∠D，BF=CE，AC∥DF．

求证：△ABC≌△DEF．

如图所示，要在公园（四边形ABCD）中建造一座音乐喷泉，喷泉位置应符合如下要求：
 
（1）到公园两个出入口A、C的距离相等；
（2）到公园两边围墙AB、AD的距离相等．
请你用尺规作图的方法确定喷泉的位置P．（不必写作法，但要保留作图痕迹）

如图，在Rt△ABC中，∠C＝90°,AC＝6,BC＝8,分别以三边为直径向上作三个半圆．

（1）AB＝      ；
（2）图中阴影部分面积＝          ．

如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为     ．

若一个等腰三角形的两边长分别为2和5，则它的周长为            ．

已知一个等腰三角形的顶角为120⁰，则它的一个底角为        度．

如图1，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的是（   ）

A．CB=CD

B．∠BAC=∠DAC

C．∠BCA=∠DCA

D．∠B=∠D=90°

如图，在直角坐标系中，已知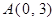、、、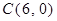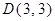，点P从C点出发，沿着折线C﹣D﹣A运动到达点A时停止，过C点作直线GC⊥PC，且与过O、P、C三点的⊙M交于点G，连接OP、PG、OD．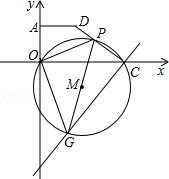

（1）直接写出∠DCO的度数；
（2）当点P在线段CD上运动时，求△OPG的最小面积；
（3）设圆心M的纵坐标为n，试探索：在点P运动的整个过程中，n的取值范围．

如图，E是BC的中点，∠1=∠2，AE=DE。

求证：AB=DC