已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于点C,D(如图).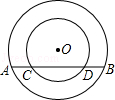
(1)求证:AC=BD;
(2)若大圆的半径R=10,小圆的半径r=8,且圆O到直线AB的距离为6,求AC的长.
如图,点D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)判断直线CD和⊙O的位置关系,并说明理由.
(2)过点B作⊙O的切线BE交直线CD于点E,若AC=2,⊙O的半径是3,求BE的长.
已知:如图,等边△ABC内接于⊙O,点P是劣弧 上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
上的一点(端点除外),延长BP至D,使BD=AP,连接CD.
(1)若AP过圆心O,如图①,请你判断△PDC是什么三角形?并说明理由;
(2)若AP不过圆心O,如图②,△PDC又是什么三角形?为什么?
以原点为圆心, 为半径的圆分别交
为半径的圆分别交 、
、 轴的正半轴于A、B两点,点P的坐标为
轴的正半轴于A、B两点,点P的坐标为 .
.
(1)如图一,动点Q从点B处出发,沿圆周按顺时针方向匀速运动一周,设经过的时间为 秒,当
秒,当 时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留
时,直线PQ恰好与⊙O第一次相切,连接OQ.求此时点Q的运动速度(结果保留 );
);
(2)若点Q按照⑴中的方向和速度继续运动,
①当 为何值时,以O、P、Q为顶点的三角形是直角三角形;
为何值时,以O、P、Q为顶点的三角形是直角三角形;
②在①的条件下,如果直线PQ与⊙O相交,请求出直线PQ被⊙O所截的弦长.


如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若 ,求大圆与小圆围成的圆环的面积.(结果保留π)
,求大圆与小圆围成的圆环的面积.(结果保留π)
如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A.与大圆相交于点B.小圆的切线AC与大圆相交于点D,且CO平分∠ACB.
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC,AD,BC之间的数量关系,并说明理由.
已知在△ABC中,∠B=90o,以AB上的一点O为圆心,以OA为半径的圆交AC于点D,交AB于点E.
(1)求证:AC·AD=AB·AE;
(2)如果BD是⊙O的切线,D是切点,E是OB的中点,当BC=2时,求AC的长.
已知在以点O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D(如图)。 
(1)求证:AC="BD"
(2)若大圆的半径 R=10,小圆的半径r="8," 且点O到直线AB的距离为6,求AC的长。
如图,PB为⊙O的切线,B为切点,直线PO交⊙O于点E,F,过点B作PO的垂线BA,垂足为点D,交⊙O于点A,延长AO与⊙O交于点C,连接BC,AF.
(1)求证:直线PA为⊙O的切线;
(2)求证:EF2=4OD•OP;
(3)若BC=6,tan∠F= ,求AC的长.
,求AC的长.
在2015年金华市体育中考中,仰卧起坐就是其中的一项选考项目.图a是小明在健身器材上进行仰卧起坐锻炼时情景,图b是小明锻炼时上半身由 位置运动到与地面垂直的
位置运动到与地面垂直的 位置时的示意图.
位置时的示意图.
已知 米,
米, 米,
米, 米.
米.
(1)求 的倾斜角
的倾斜角 的度数(精确到
的度数(精确到 );
);
(2)若测得 米,试计算小明头顶由
米,试计算小明头顶由 点运动到
点运动到 点的路径弧MN的长度(精确到0.01米).
点的路径弧MN的长度(精确到0.01米).
(参考数据:sin18°≈ ,cos72°≈
,cos72°≈ ,tan17°≈
,tan17°≈ ,
, )
)
如图,AB是⊙O的弦,半径OA=20cm,∠AOB=120o.求:
(1)△OAB的面积.
(2)阴影部分的面积.(精确到1cm2)
七年级我们学过三角形的相关知识,在动手实践的过程中,发现了一个基本事实:
三角形的三条高(或三条高所在直线)相交于一点.
其实,有很多八年级、九年级的问题均可用此结论解决.
【运用】如图,已知:△ABC的高AD与高BE相交于点F,且∠ABC=45°,过点F作FG∥BC交AB于点G,求证:FG+CD=BD.
小方同学在解答此题时,利用了上述结论,她的方法如下:
连接CF并延长,交AB于点M,
∵△ABC的高AD与高BE相交于点F,
∴CM为△ABC的高.
(请你在下面的空白处完成小方的证明过程.)
【操作】如图AB是圆的直径,点C在圆内,请仅用无刻度的直尺画出△ABC中AB边上的高.
试题篮
()