如图,在
中,
是直径,点
是
上一点且
,过点
作
的切线
交
的延长线于点
,
为
的中点,连接
,
.

(1)求证:四边形
是平行四边形;
(2)已知图中阴影部分面积为
,求
的半径
.
如图,已知⊙ 的直径AB=12cm,AC是⊙
的直径AB=12cm,AC是⊙ 的弦,过点C作⊙
的弦,过点C作⊙ 的切线交BA的延长线于点P,连接BC
的切线交BA的延长线于点P,连接BC
(1)求证:∠PCA=∠B
(2)已知∠P=40°,点Q在优弧ABC上,从点A开始逆时针运动到点C停止(点Q与点C不重合),当△ABQ与△ABC的面积相等时,求动点Q所经过的弧长
(1)已知:如图1,在矩形ABCD中,点E,F分别在AB,CD边上,BE=DF,连接CE,AF.求证:AF=CE.
(2)如图2,AB切⊙O于点B,OA=2,∠OAB=30°,弦BC∥OA.求:劣弧BC的长.(结果保留π)
如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.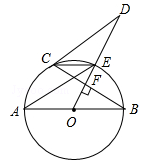
(1)求证:直线CD为⊙O的切线;
(2)若AB=5,BC=4,求线段CD的长.
(本小题满分10分)已知,如图所示,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E,若DE=6cm,AE=3cm,求⊙O的半径.
(本小题满分7分)完成下列各题:
(1)如图,△ABC和△ADE中,∠BAC=∠DAE,AB=AE,AC=AD,连接BD,CE,求证:△ABD≌△AEC.
(2)如图,AB是⊙O的弦,∠OAB=20°,求弦AB所对的圆周角的度数.
如图,已知AB是⊙O的直径,C为⊙O外一点,连结CO并延长交⊙O于点D、E,连结BD并延长交AC于点F,连结AD,∠DAF=∠B.
(1)求证:CA是⊙O的切线;
(2)若AB=6,CA=4,求CD的长;
(3)在(2)的条件下,求tan∠CDF的值.
如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 上一点,
上一点, 是
是 的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
的中点,过点D作⊙O的切线,与AB,AC的延长线分别交于点E,F,连结AD.
(1)求证:AF⊥EF;
(2)若 ,AB=5,求线段BE的长.
,AB=5,求线段BE的长.
如图,AB是⊙O的直径,点E是 上一点,∠DAC=∠AED.
上一点,∠DAC=∠AED.
(1)求证:AC是⊙O的切线;
(2)若点E是 的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
的中点,连结AE交BC于点F,当BD=5, CD=4时,求DF的值.
(本小题满分12分)如图,AC是⊙O的直径,点B在⊙O上,∠ACB=30°.
(1)利用尺规作∠ABC的平分线BD,交AC于点E,交⊙O于点D,连接CD(保留作图痕迹,不写作法);
(2)在(1)所作的图形中,求 与
与 的面积之比.
的面积之比.
如图,⊙O是△ABC的外接圆,AB是直径,作OD∥BC与过点A的切线交于点D,连接DC并延长交AB的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AE=6,CE= ,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
,求线段CE、BE与劣弧BC所围成的图形面积.(结果保留根号和π)
如图,AB是⊙O的直径,点C在⊙O上,过点C作⊙O的切线CM.
(1)求证:∠ACM=∠ABC;
(2)延长BC到D,BC=CD,连接AD与CM交于点E,若⊙O的半径为3,ED=2,求△ACE的外接圆的直径.
如图,点 是半圆
是半圆 的半径
的半径 上的动点,作
上的动点,作 于
于 .点
.点 是半圆上位于
是半圆上位于 左侧的点,连结
左侧的点,连结 交线段
交线段 于
于 ,且
,且 .
.
(1)求证: 是⊙O的切线.
是⊙O的切线.
(2)若⊙O的半径为 ,
, ,设
,设 .
.
①求 关于
关于 的函数关系式.
的函数关系式.
②当 时,求
时,求 的值.
的值.
(本小题满分10分)已知等腰△ABC和⊙M,且AB=AC.
(1)如图l,若⊙M与BA的延长线AK及边AC均相切,求证:AM∥BC;
(2)如图2,若∠B=60°,⊙M与BA的延长线AK、BC的延长线CE及边AC均相切,求证:四边形ABCM是平行四边形.
试题篮
()