如图,点A、B、C是⊙O上的三点,AB∥OC.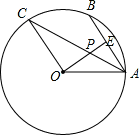
(1)求证:AC平分∠OAB;
(2)过点O作OE⊥AB于点E,交AC于点P.若AB=2,∠AOE=30°,求PE的长.
AB是⊙O的直径,AD与⊙O相交,点C是⊙O上一点,经过点C的直线交AD于点E.
(1)如图1 ,若AC平分∠BAD,CE⊥AD于点E,求证:CE是⊙O的切线;
(2)如图2,若CE是⊙O的切线,CE⊥AD于点E,AC是∠BAD的平分线吗?说明理由;
(3)如图3,若CE是⊙O的切线,AC平分∠BAD,AB=8,AC=6,求AE的长度.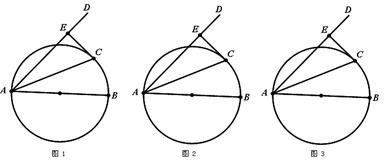
如图,四边形ABCD内接于⊙O,BC是直径,∠BAD=120°,AB=AD.
(1)求证:四边形ABCD是等腰梯形;
(2)已知AC=6,求阴影部分的面积.
如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是△ABC内一点,连结AD,将线段AD绕点A逆时针旋转一定角度得到线段AE使∠BAD=∠CAE(E在AC右侧),连结BD,CE.
(1)求证:BD=CE;
(2)若AD=2,求点D绕点A旋转到点E所经过的路径长.
如图,在平面直角坐标系中,顶点为(4,﹣1)的抛物线交y轴于A点,交x轴于B,C两点(点B在点C的左侧),已知A点坐标为(0,3).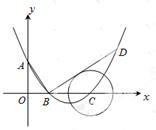
(1)求此抛物线的解析式
(2)过点B作线段AB的垂线交抛物线于点D,如果以点C为圆心的圆与直线BD相切,请判断抛物线的对称轴与⊙C有怎样的位置关系,并给出证明;
(3)已知点P是抛物线上的一个动点,且位于A,C两点之间,问:当点P运动到什么位置时,△PAC的面积最大?并求出此时P点的坐标和△PAC的最大面积.
如图,AC是⊙O的直径,点B,D在⊙O上,点E在⊙O外,∠EAB=∠D=30°.
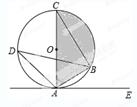
(1)求证:AE是⊙O的切线;
(2)当AB=3时,求图中阴影部分的面积(结果保留根号和π).
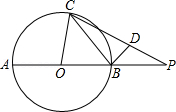
如图,AB是⊙O的直径,延长AB至P,使BP=OB,BD垂直于弦BC,垂足为点B,点D在PC上.设∠PCB=α,∠POC=2β.求证:tanα•tanβ=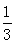 .
.
如图,△ABC中,AB=4,BC=3,以C为圆心,CB的长为半径的圆和AC交于点D,连接BD,若∠ABD= ∠C.
∠C.

(1)求证:AB是⊙C的切线;
(2)求△DAB的面积.
如图,在矩形ABCD的对角线AC上有一动点O,以OA为半径作⊙O交AD、AC于点E、F,连结CE.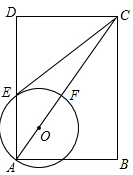
(1)若CE恰为⊙O的切线,求证:∠ACB=∠DCE;
(2)在(1)的条件下,若AB=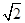 ,BC=2,求⊙O的半径.
,BC=2,求⊙O的半径.
如图,已知AB是⊙O的直径,直线CD与⊙O相切于点C,AC平分∠DAB.
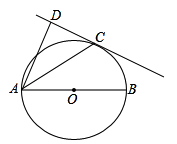
(1)求证:AD⊥DC;
(2)若AD=2,AC= ,求AB的长.
,求AB的长.
AH是⊙O的直径,AE平分∠FAH,交⊙O于点E,过点E的直线FG⊥AF,垂足为F,B为直径OH上一点,点E、F分别在矩形ABCD的边BC和CD上.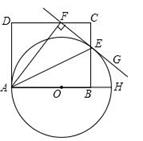
(1)求证:直线FG是⊙O的切线;
(2)若CD=10,EB=5,求⊙O的直径.
如图:AB是⊙O的直径,以OA为直径的⊙O1与⊙O的弦AC相交于D,DE⊥OC,垂足为E。
(1)求证:AD=DC
(2)求证:DE是的切线
(3)如果OE=EC,请判断四边形O1OED是什么四边形,并证明你的结论。
试题篮
()